Introduction to ggplot2
IBPM-CNR
2024-06-26
Introduction to ggplot2
What is ggplot2?
- Part of the
tidyverse - Designed for creating complex plots from data in a data frame
- Based on the Grammar of Graphics: a coherent system for describing and building graphs
The Grammar of Graphics
- Visualisation concept created by Leland Wilkinson (1999)
- to define the basic elements of a statistical graphic
- Adapted for R by Hadley Wickham (2009)
- consistent and compact syntax to describe statistical graphics
- highly modular as it breaks up graphs into semantic components
Introduction to ggplot2
Why use ggplot2?
- High customization
- Elegant and versatile plots
- Consistent syntax
Basic ggplot2 Syntax
- data: The data frame containing the variables
- aes: Aesthetic mappings, describing how variables are mapped to visual properties
- geom: Geometric objects, representing what is actually displayed (e.g., points, lines)
Anatomy of a ggplot2 call
ggplot(
data = [dataframe],
mapping = aes(
x = [var_x], y = [var_y],
color = [var_for_color],
shape = [var_for_shape],
...
)
) +
geom_[some_geom](
mapping = aes(
color = [var_for_geom_color],
...
)
) +
... # other geometries
scale_[some_axis]_[some_scale]() +
facet_[some_facet]([formula]) +
... # other optionsCreating a Basic Plot
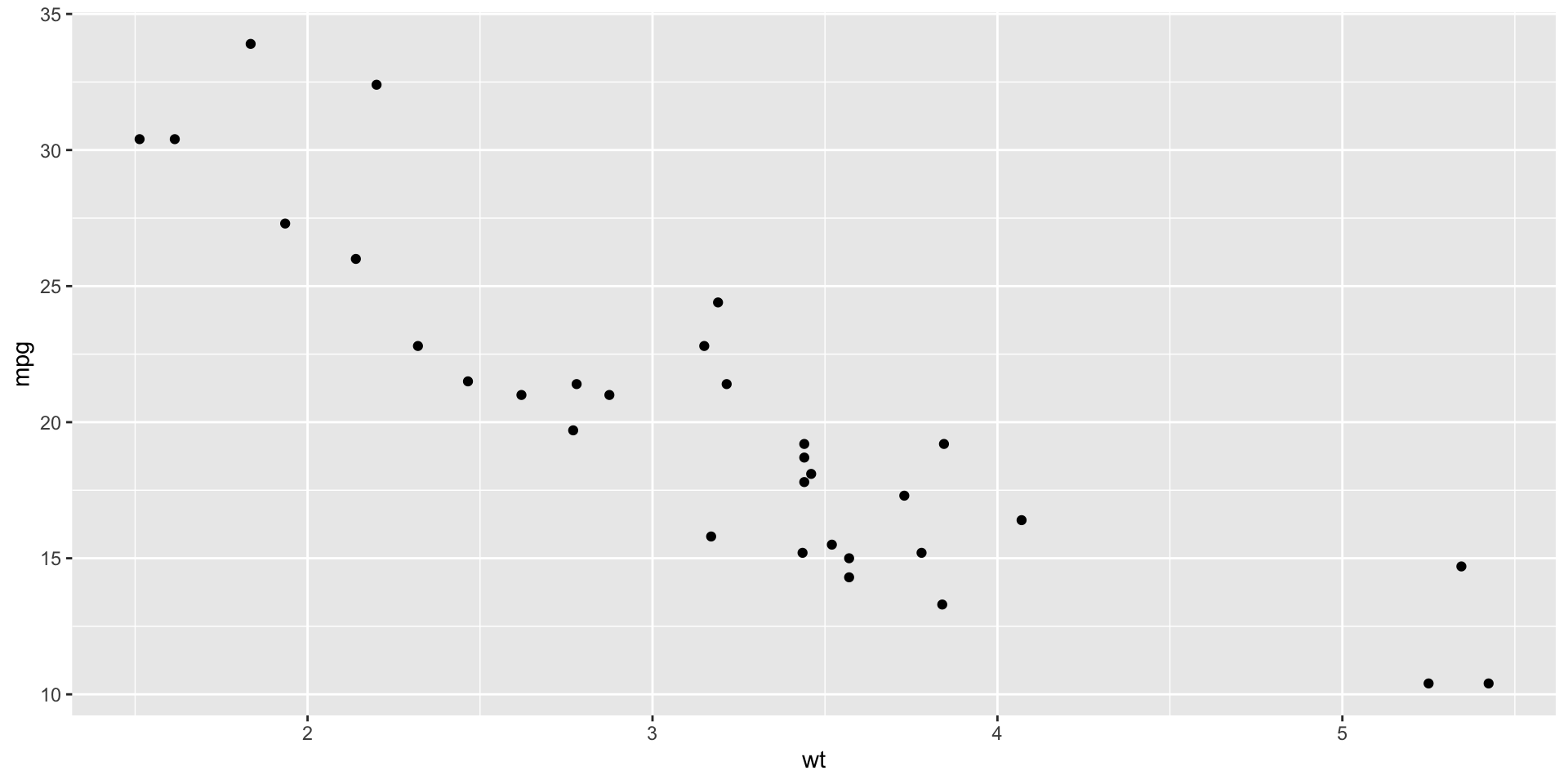
- ggplot() initializes the plot
- aes() maps the variables
- geom_point() adds a layer of points to the plot
Adding Aesthetics
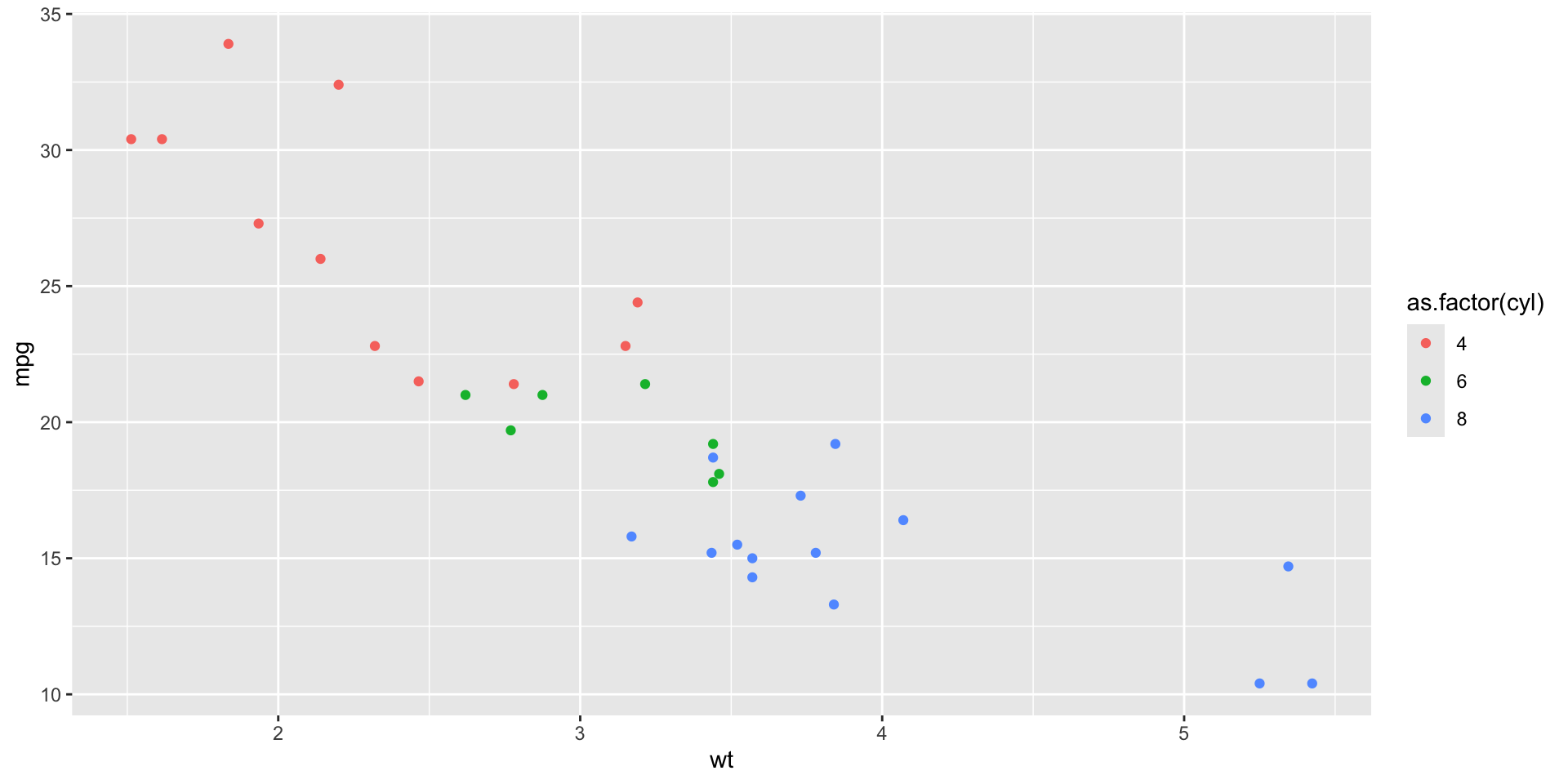
- color: Differentiates points by cylinder count
- Aesthetics can also include size, shape, and more
Titles and Labels
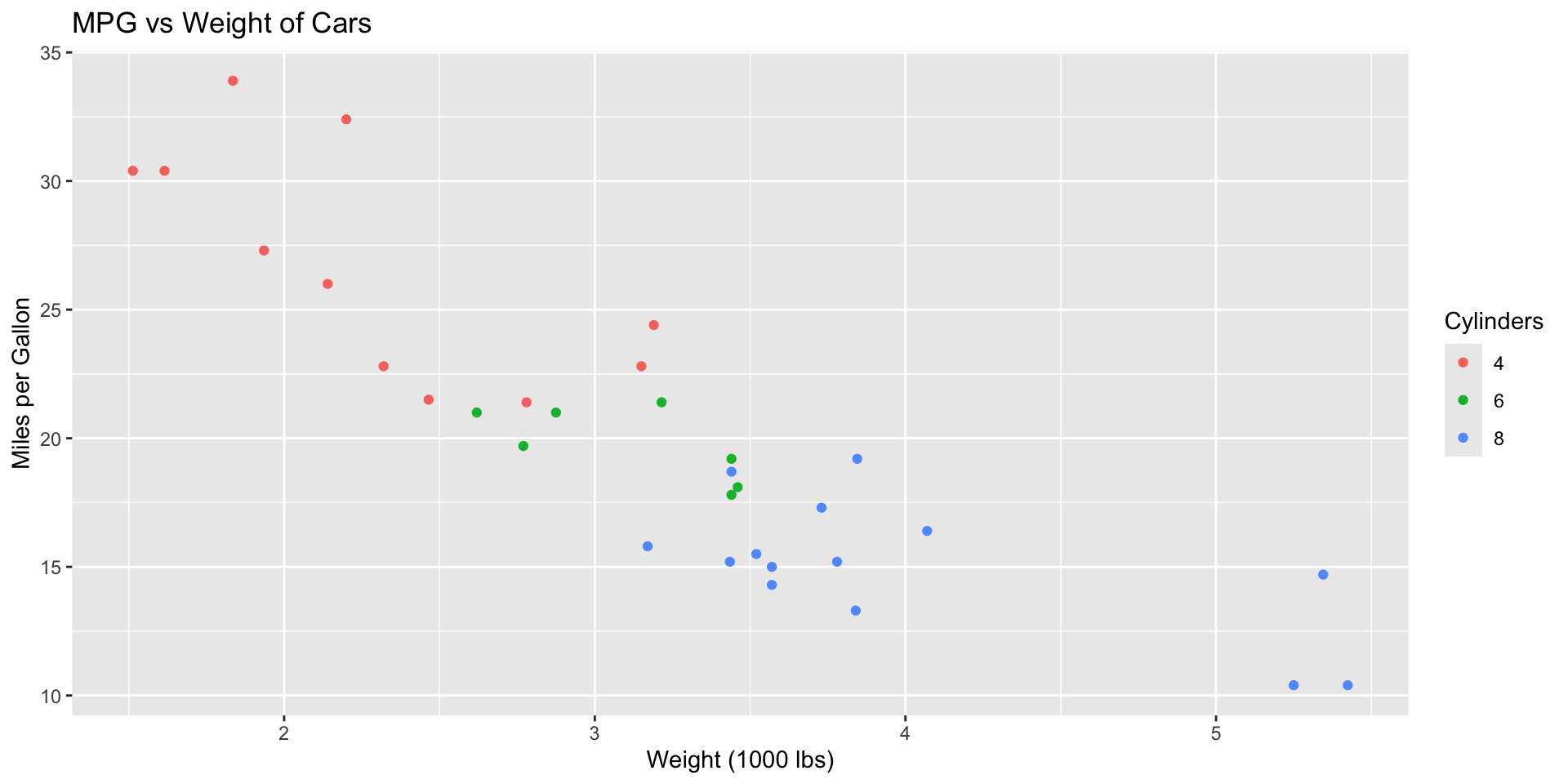
- ggtitle(): Adds a plot title
- xlab() and ylab(): Label the axes
- labs(): Additional labels, such as legends
Boxplots and Histograms
Boxplot Example:
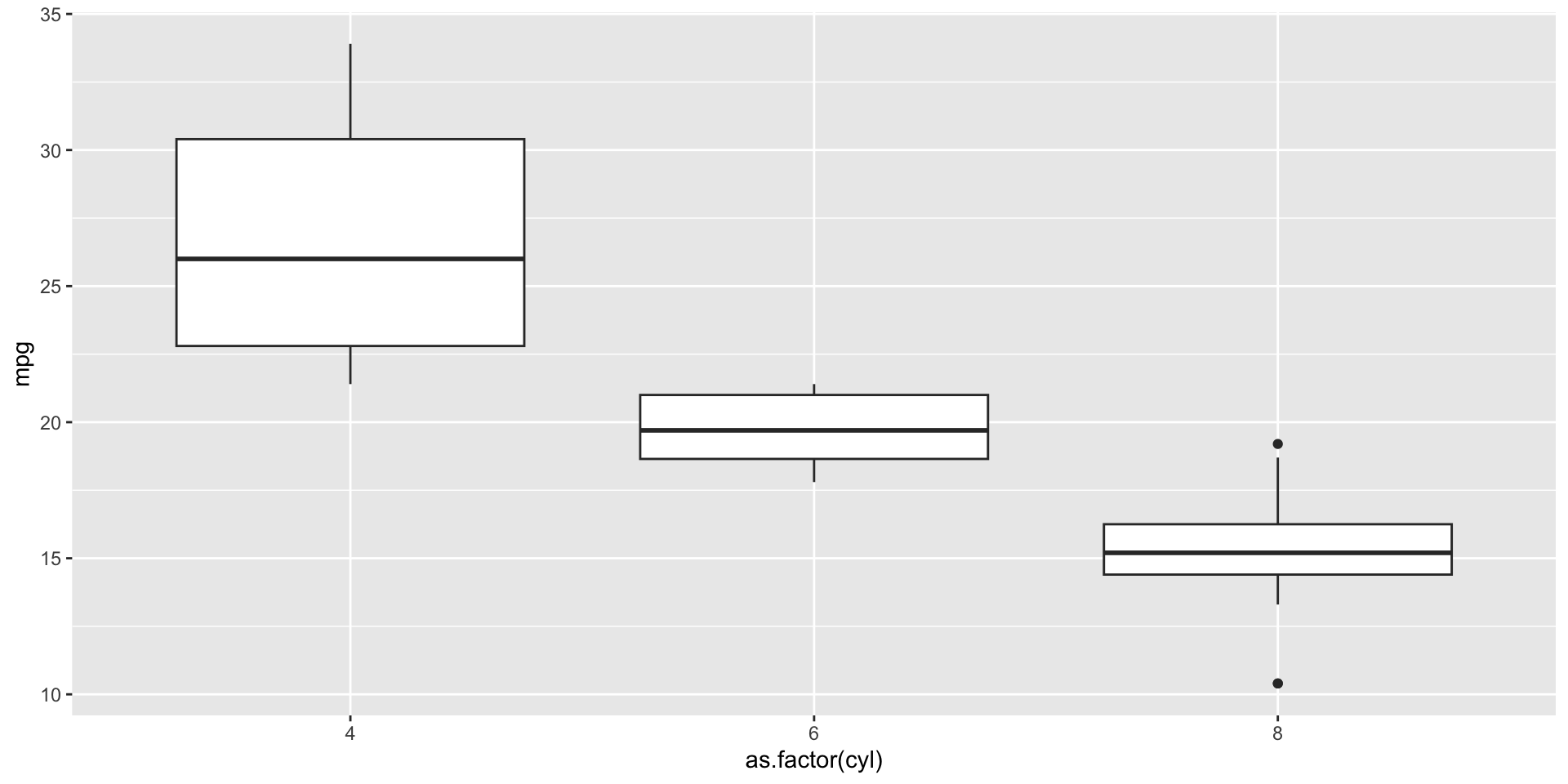
Histogram Example:
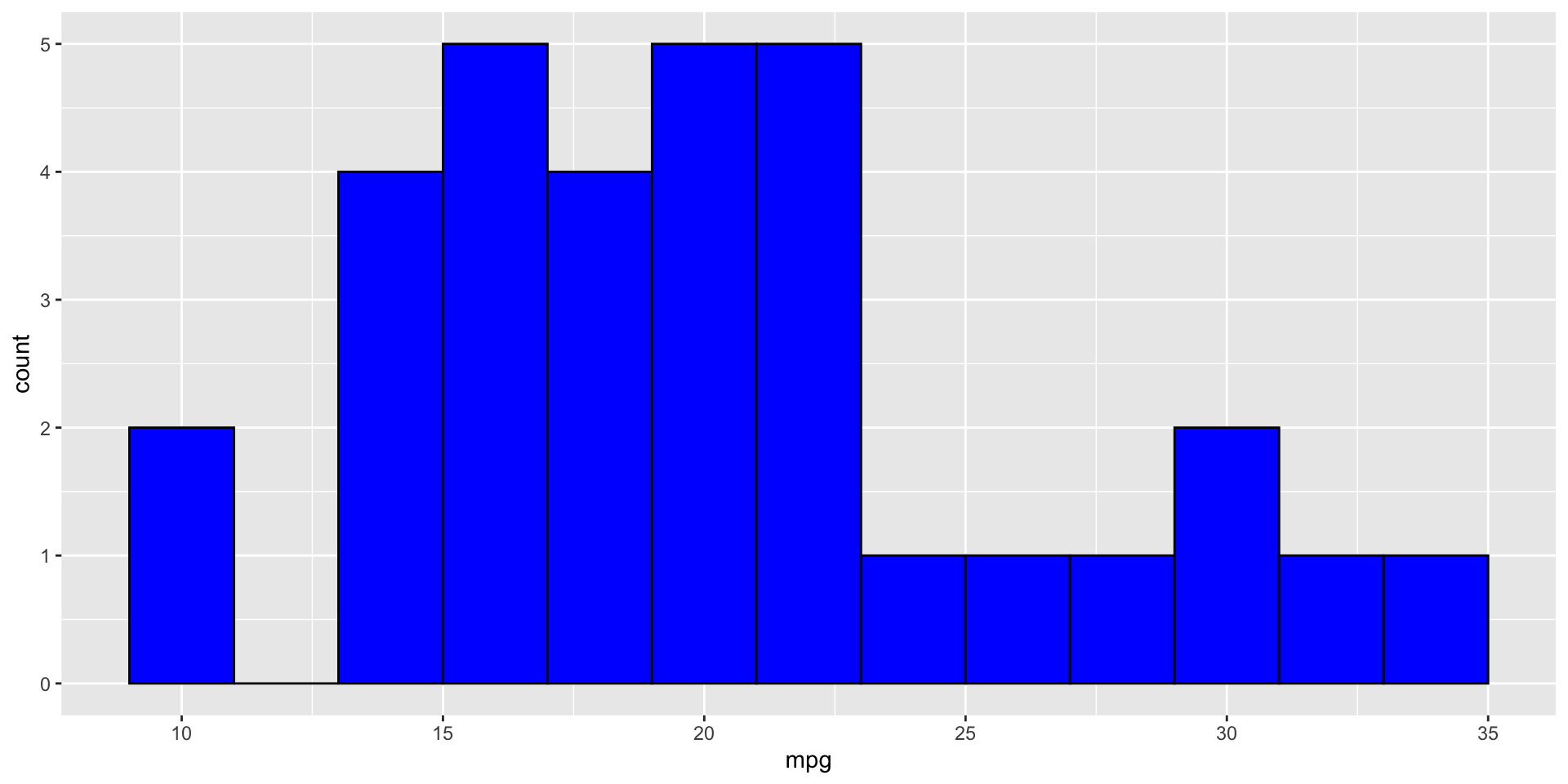
- geom_boxplot(): Creates boxplots
- geom_histogram(): Creates histograms with specified bin width
Faceting
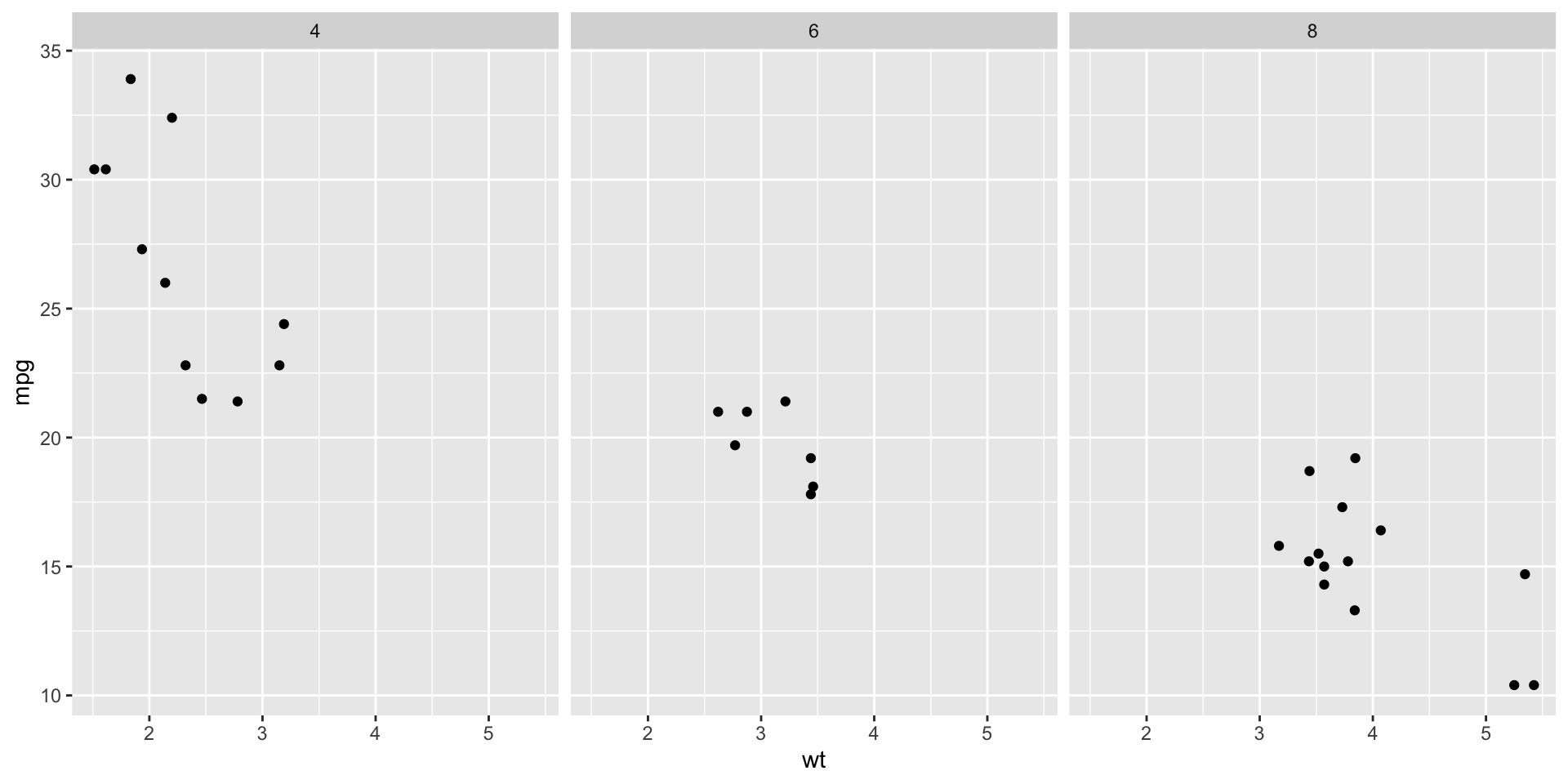
- facet_wrap(~ variable): Creates a separate plot for each level of the variable
Customizing Themes
- theme_minimal(): Applies a minimal theme
- Other themes include theme_classic(), theme_dark(), etc.
Saving Plots
- ggsave(): Saves the last plot to a file
- Can specify file format (PDF, PNG, …), dimensions, and more
Diamonds
# A tibble: 1,000 × 10
carat cut color clarity depth table price x y z
<dbl> <ord> <ord> <ord> <dbl> <dbl> <int> <dbl> <dbl> <dbl>
1 1.5 Very Good F SI2 58.5 55 9236 7.51 7.56 4.41
2 0.49 Fair E VVS2 65.5 58 1705 4.91 4.86 3.2
3 0.32 Very Good D SI1 63 57 526 4.35 4.38 2.75
4 1.44 Premium I VS1 62.6 59 8426 7.08 7.14 4.45
5 1.02 Very Good G SI2 62.9 59 4291 6.38 6.4 4.02
6 0.32 Ideal E VVS2 62 55 842 4.38 4.4 2.72
7 0.27 Ideal E VVS2 62.2 55 622 4.12 4.17 2.58
8 0.91 Premium E SI1 62.6 58 4211 6.14 6.17 3.85
9 1.02 Ideal F VS1 61.5 56 7916 6.47 6.5 3.99
10 0.7 Very Good G VS1 59.2 58 2676 5.8 5.83 3.44
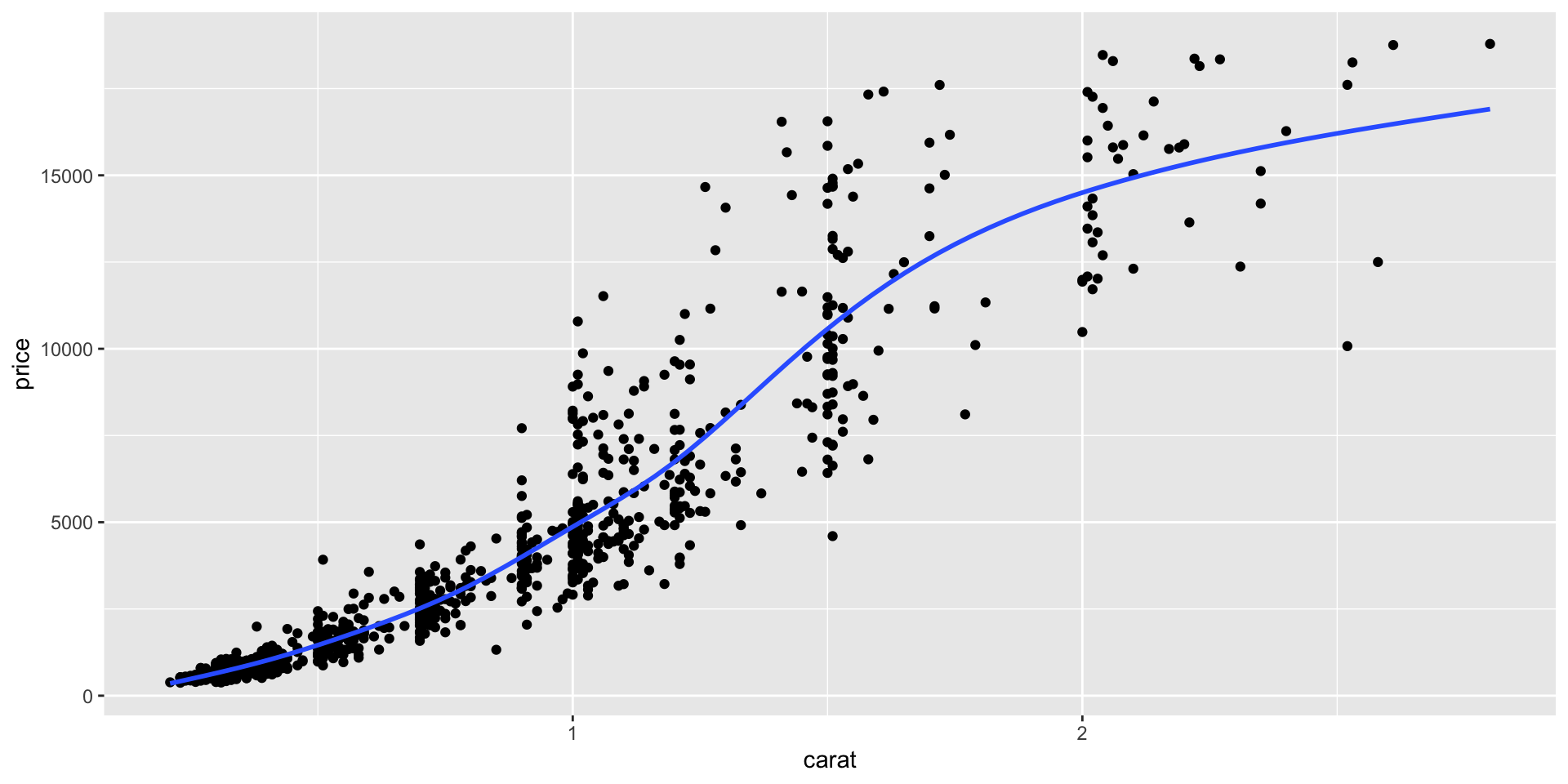
# ℹ 990 more rowsExample 1
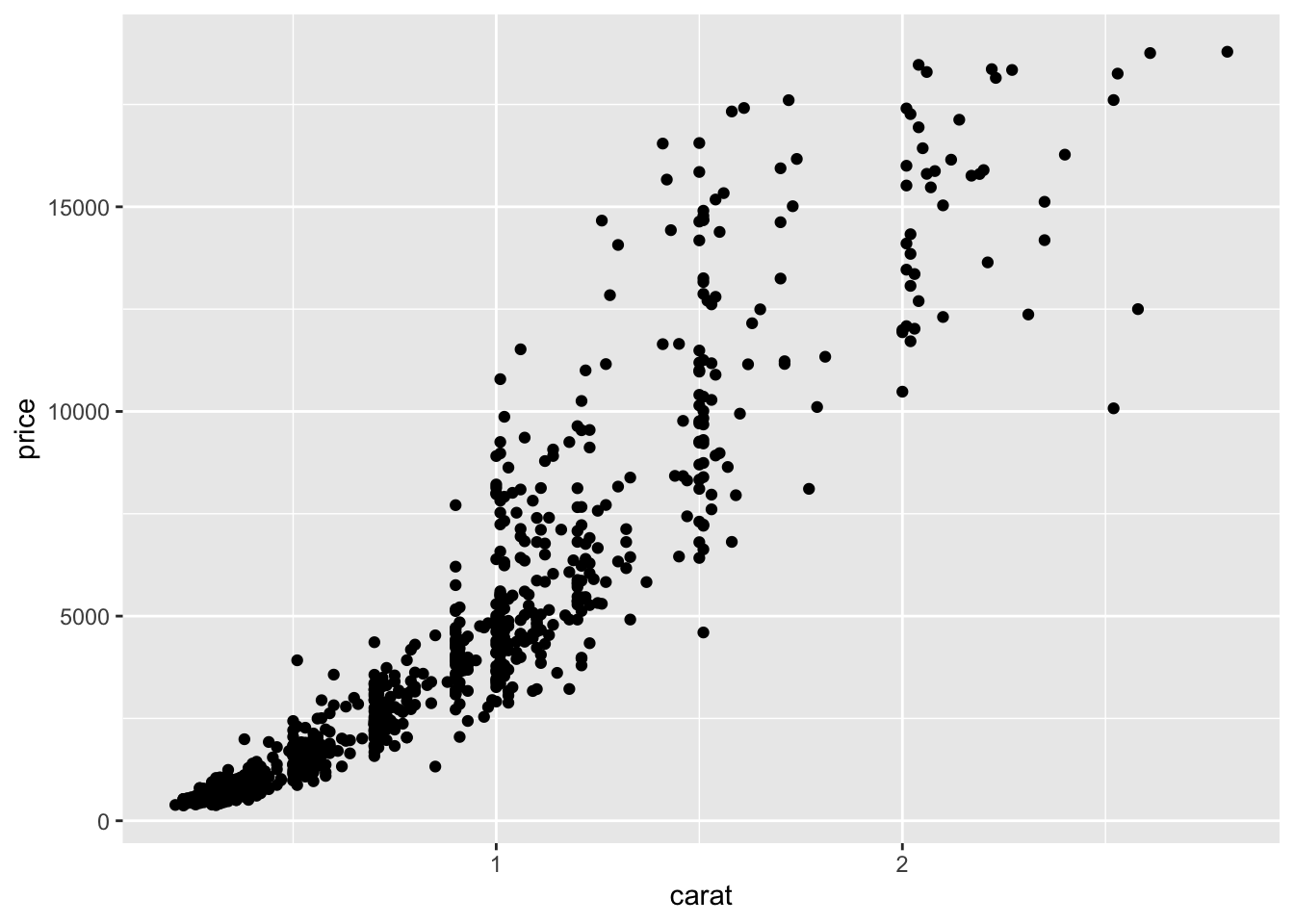
- Which data are used as an input?
- Are the variables transformed before plotting?
- What geometric objects are used to represent the data?
- What variables are mapped onto which aesthetic attributes?
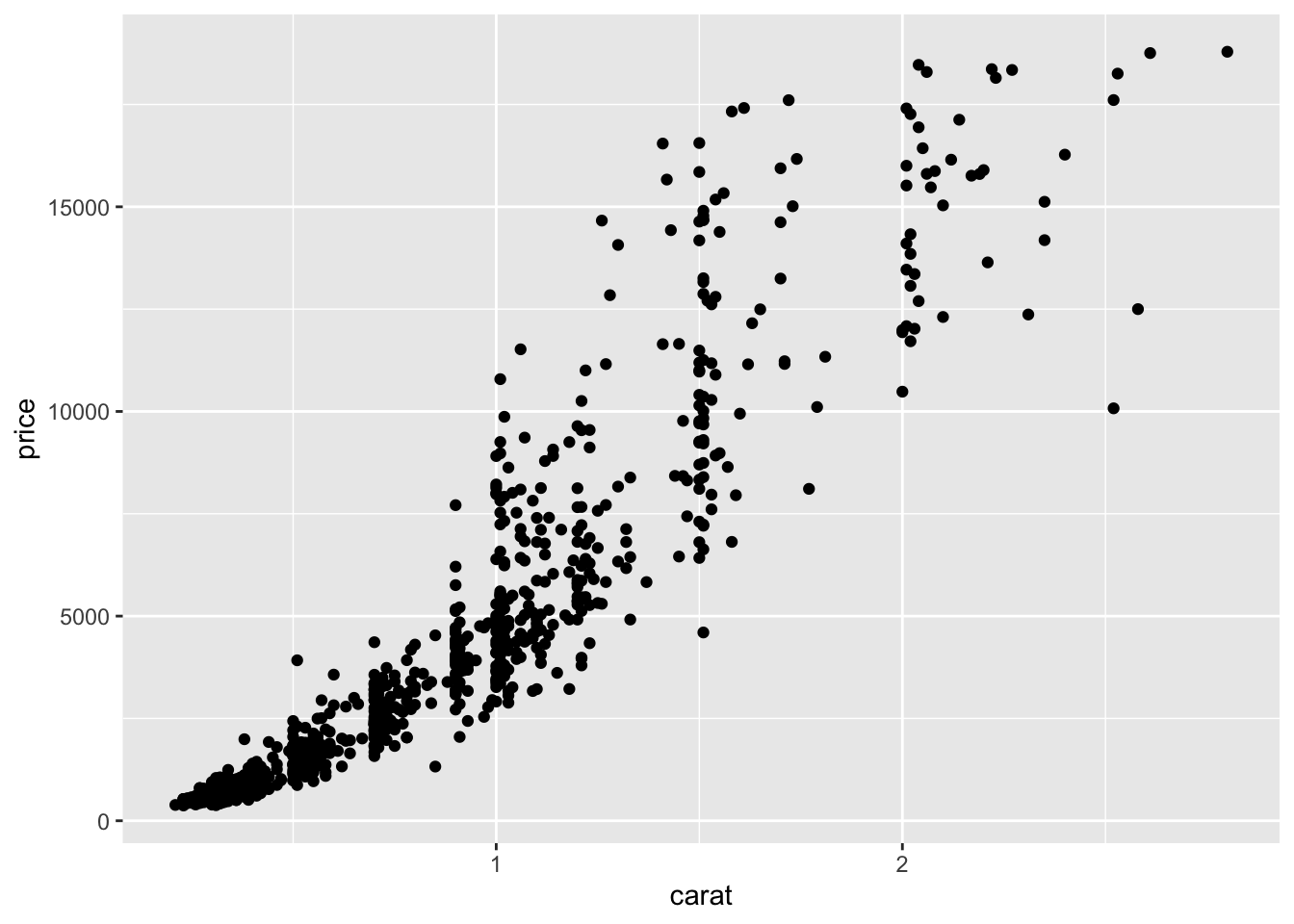
Altering aesthetics
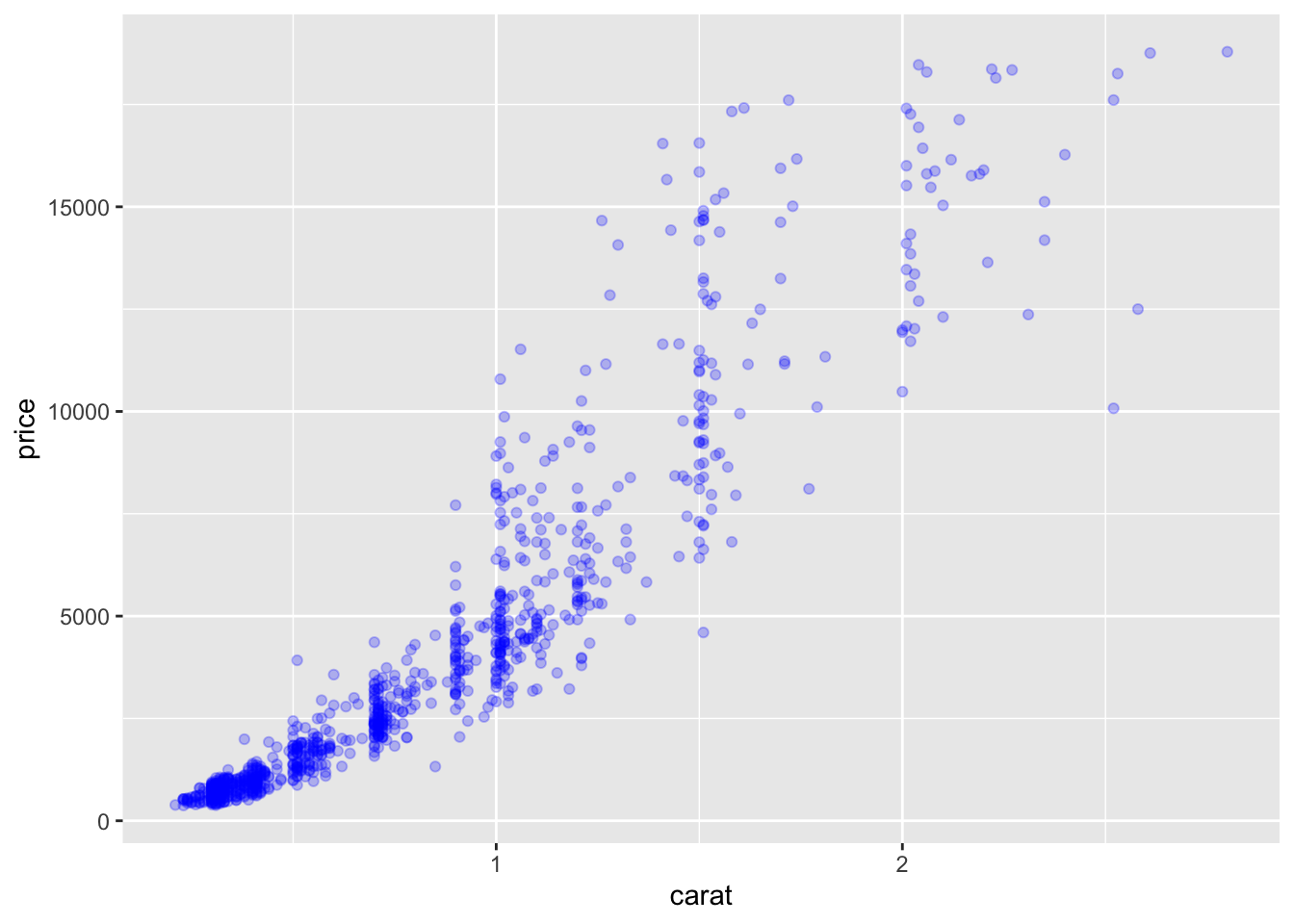
- How did the plot change?
- Are these changes based on data or are the changes based on stylistic choices for the geometric objects?
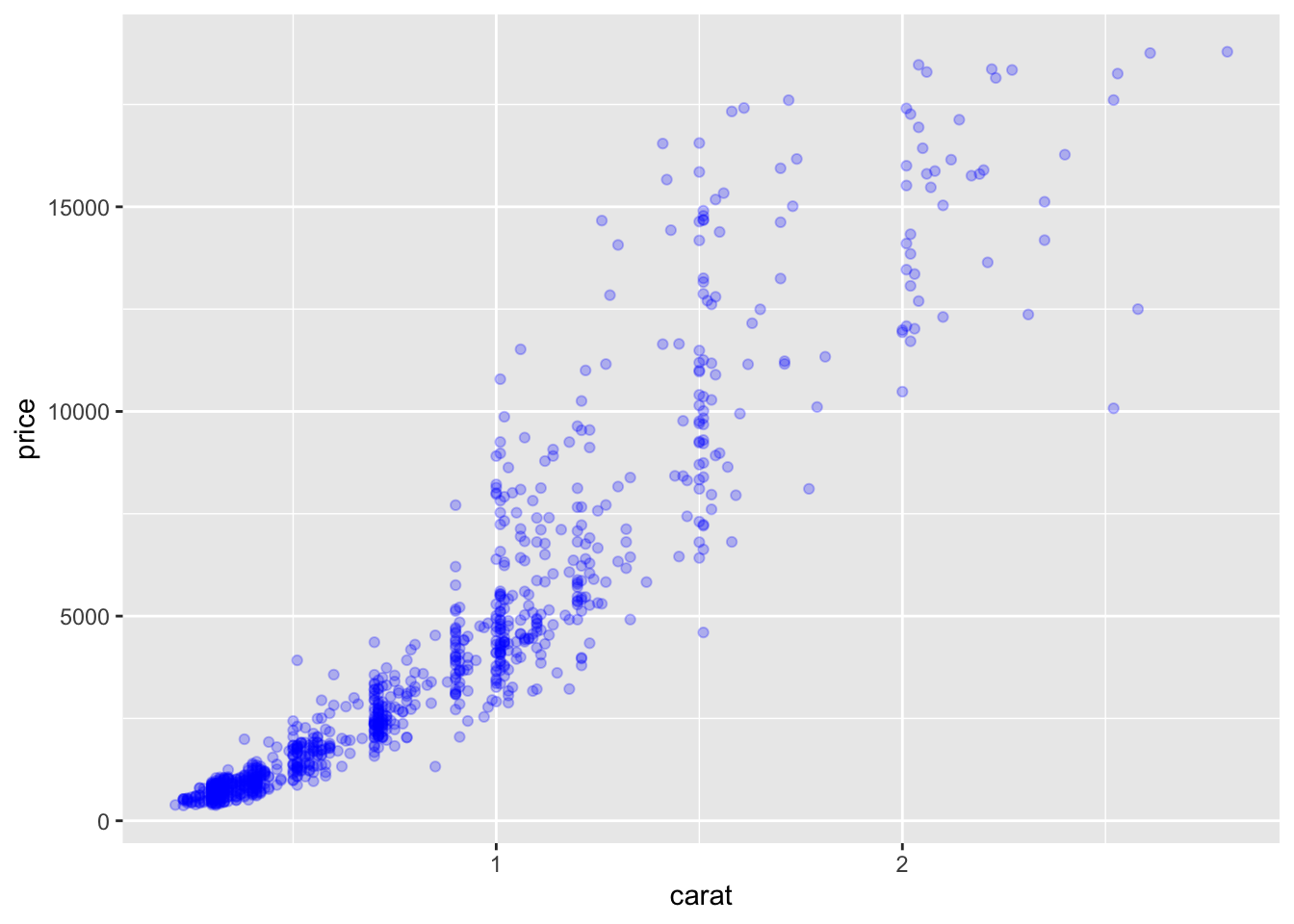
Example 2
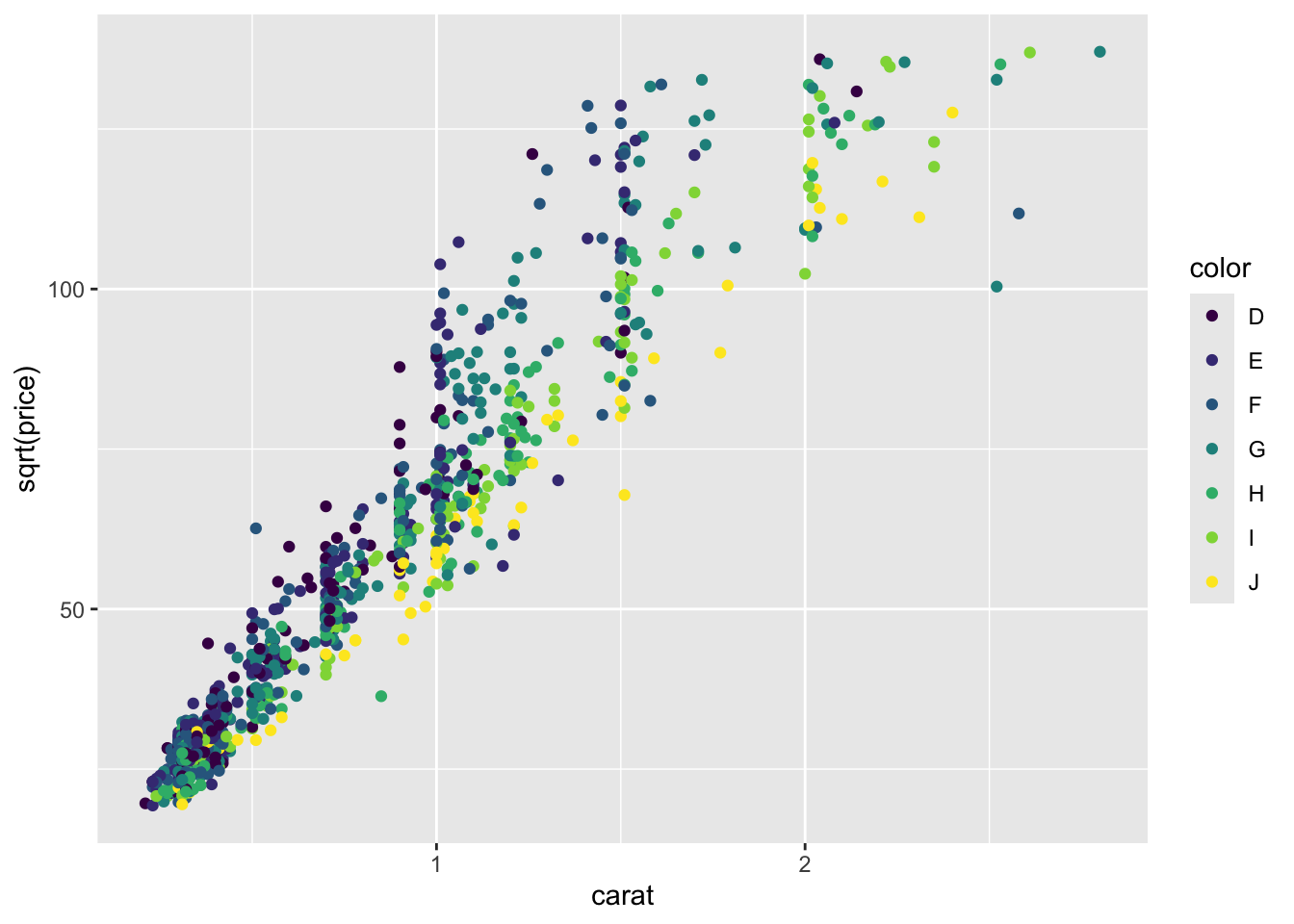
- Which data are used as an input?
- Are the variables transformed before plotting?
- What geometric objects are used to represent the data?
- What variables are mapped onto which aesthetic attributes?
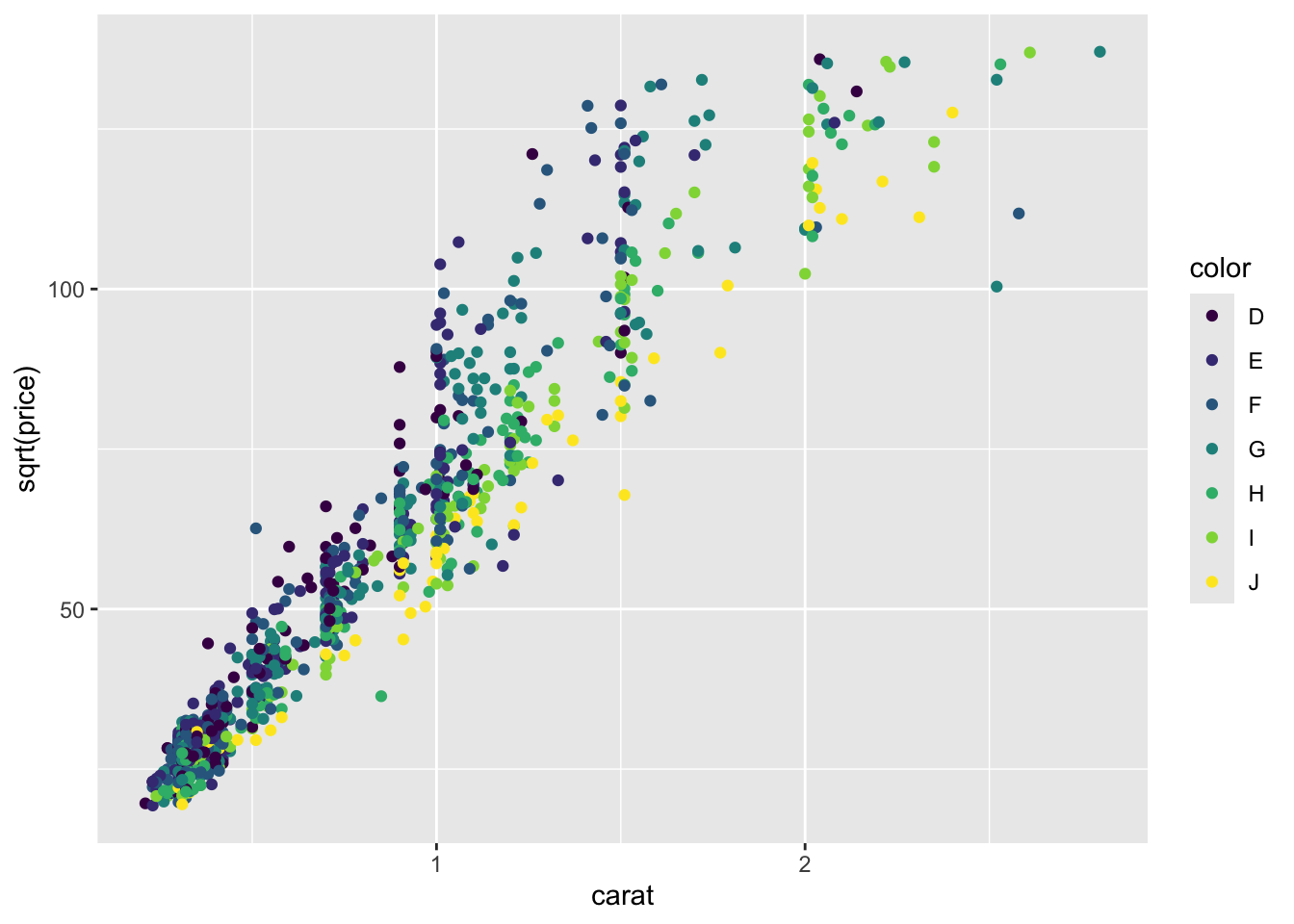
Example 3
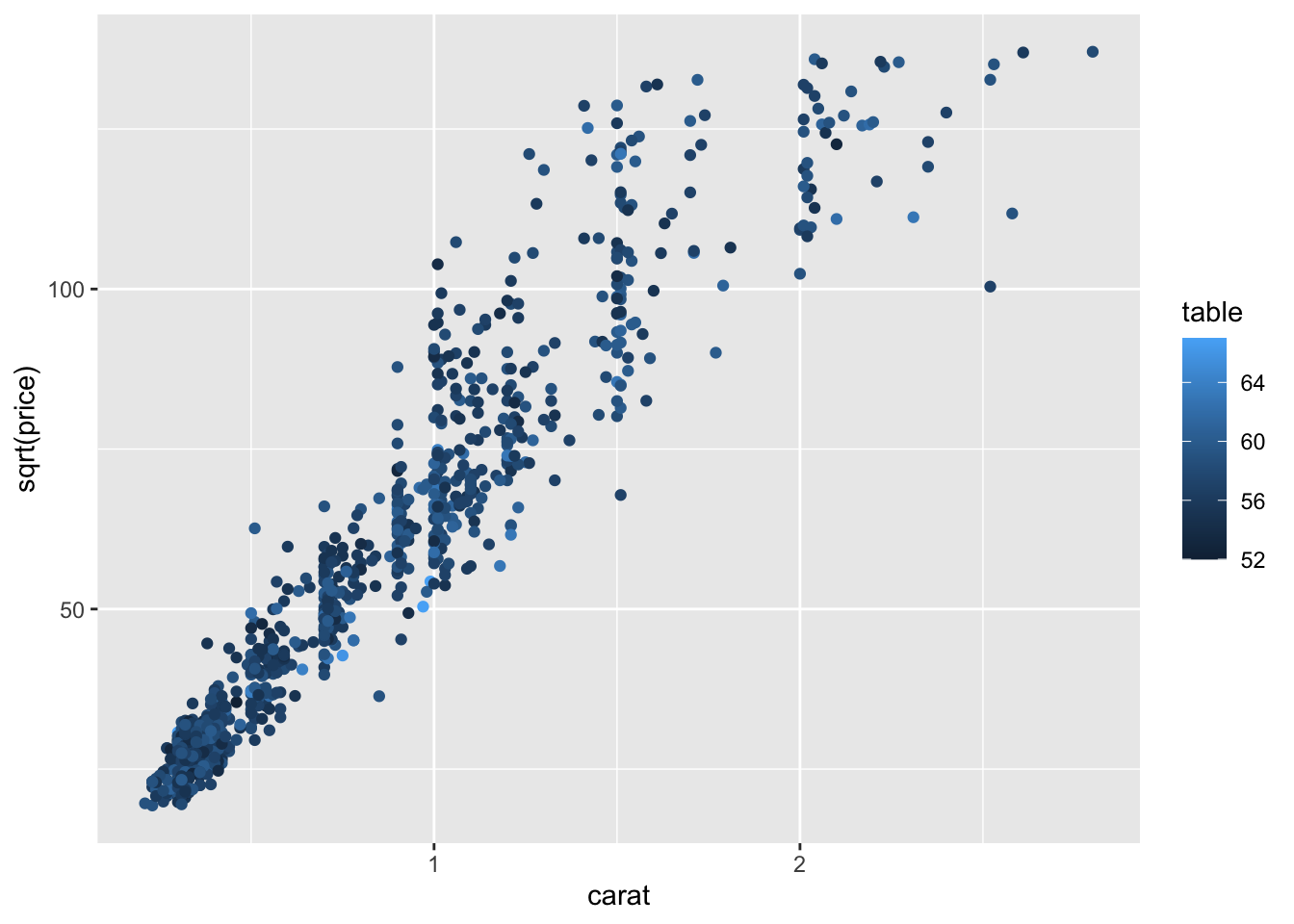
- Which data are used as an input?
- Are the variables transformed before plotting?
- What geometric objects are used to represent the data?
- What variables are mapped onto which aesthetic attributes?
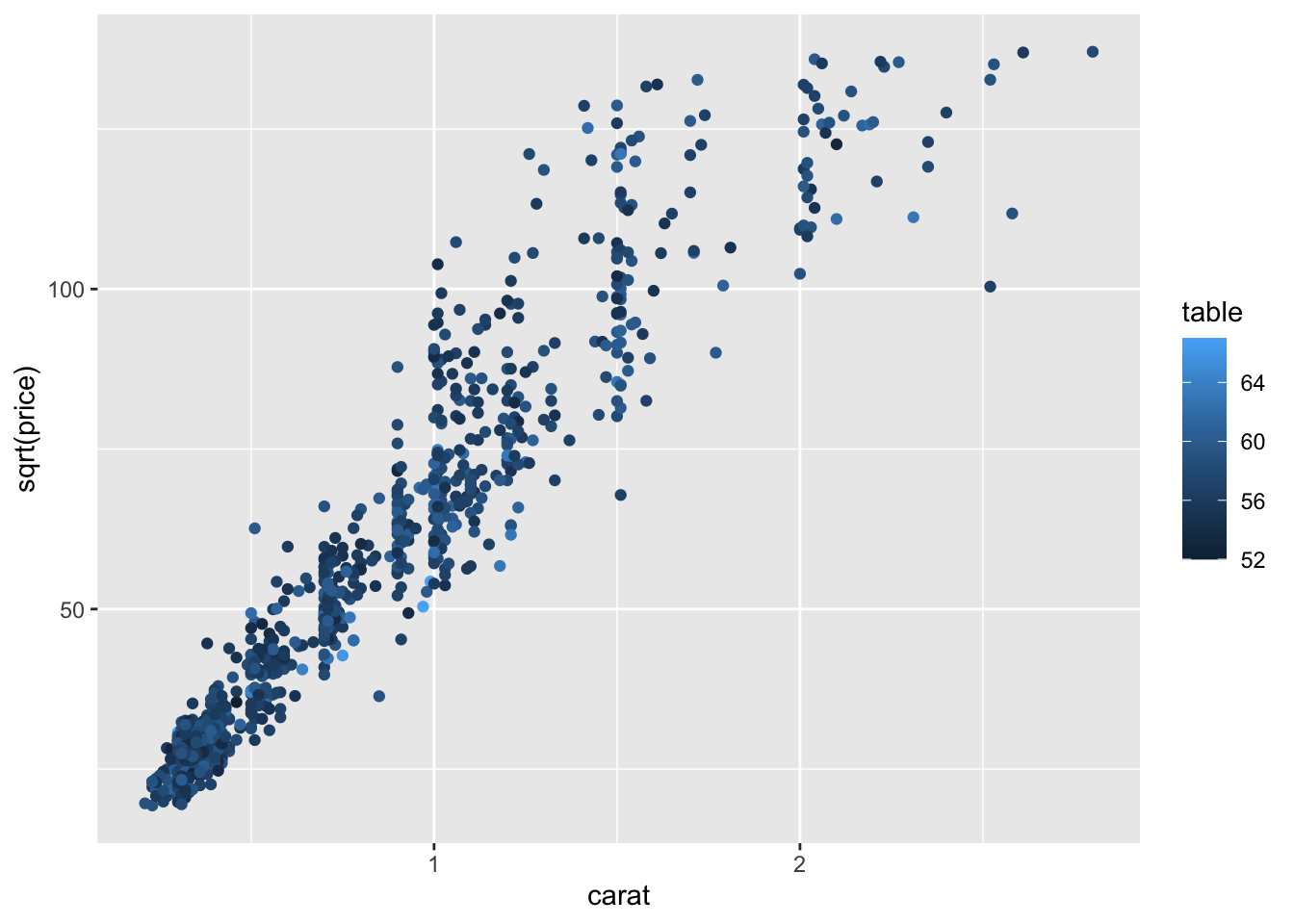
Example 4
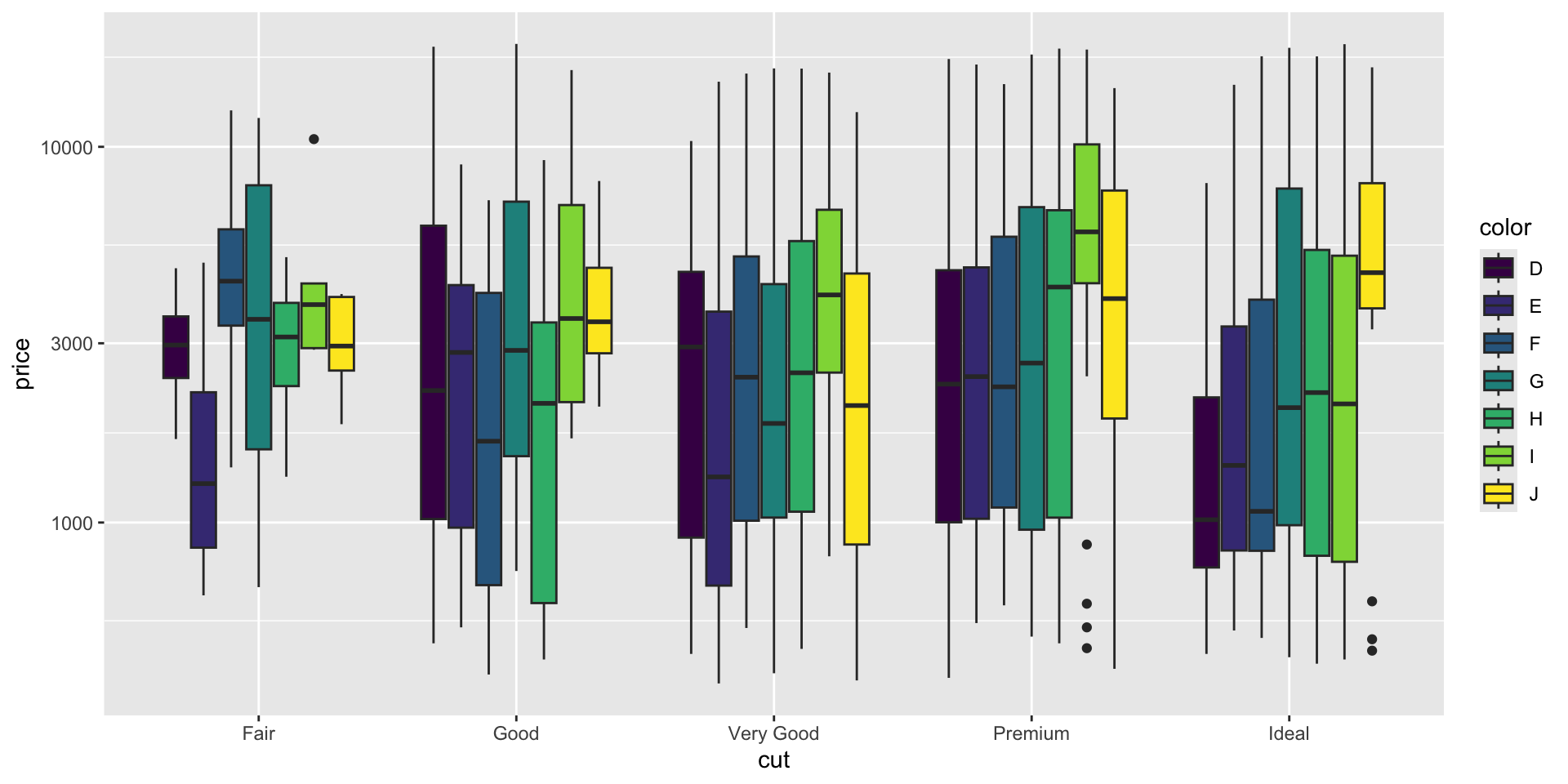
- Which data are used as an input?
- Are the variables transformed before plotting?
- What geometric objects are used to represent the data?
- What variables are mapped onto which aesthetic attributes?
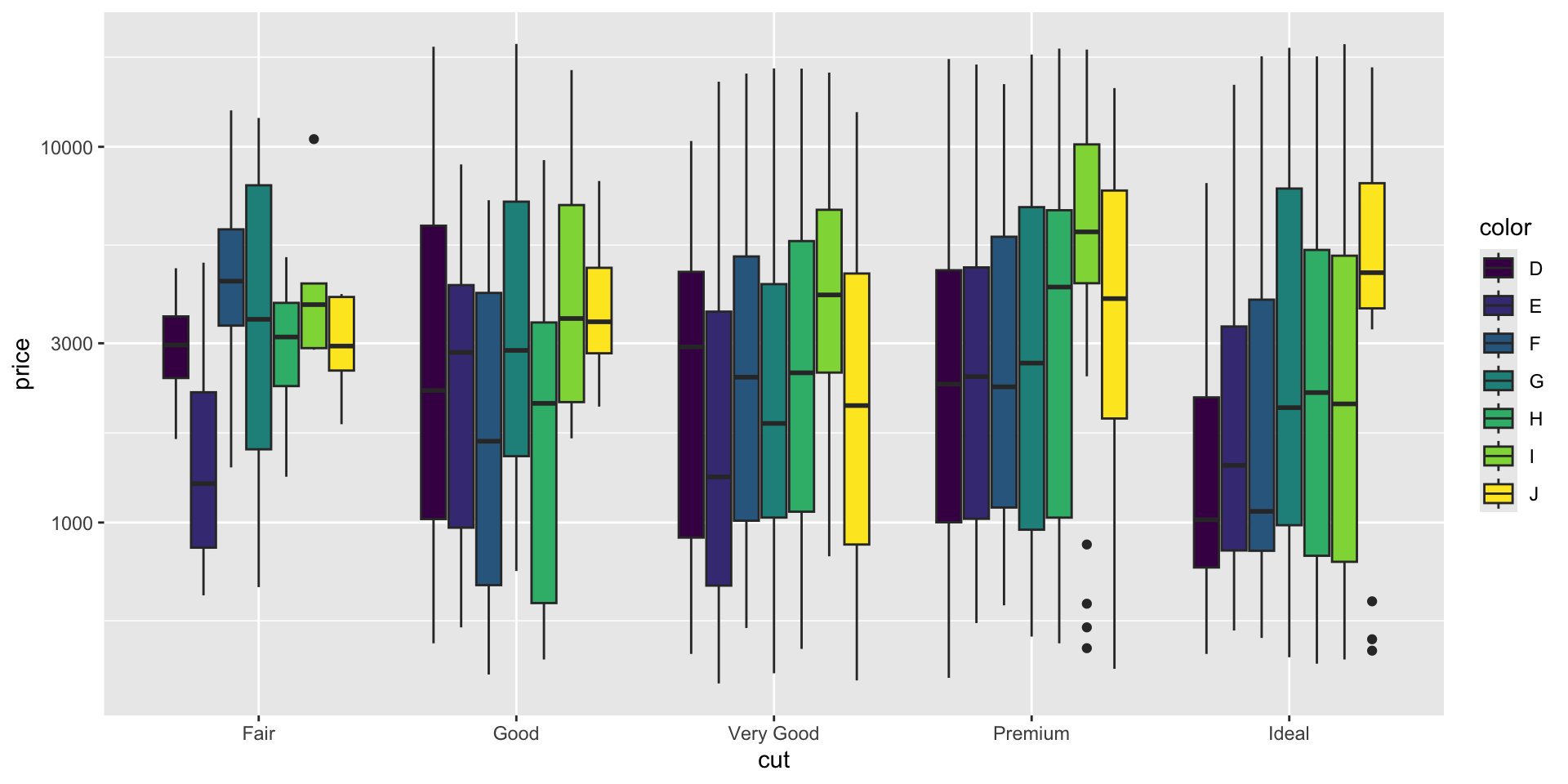
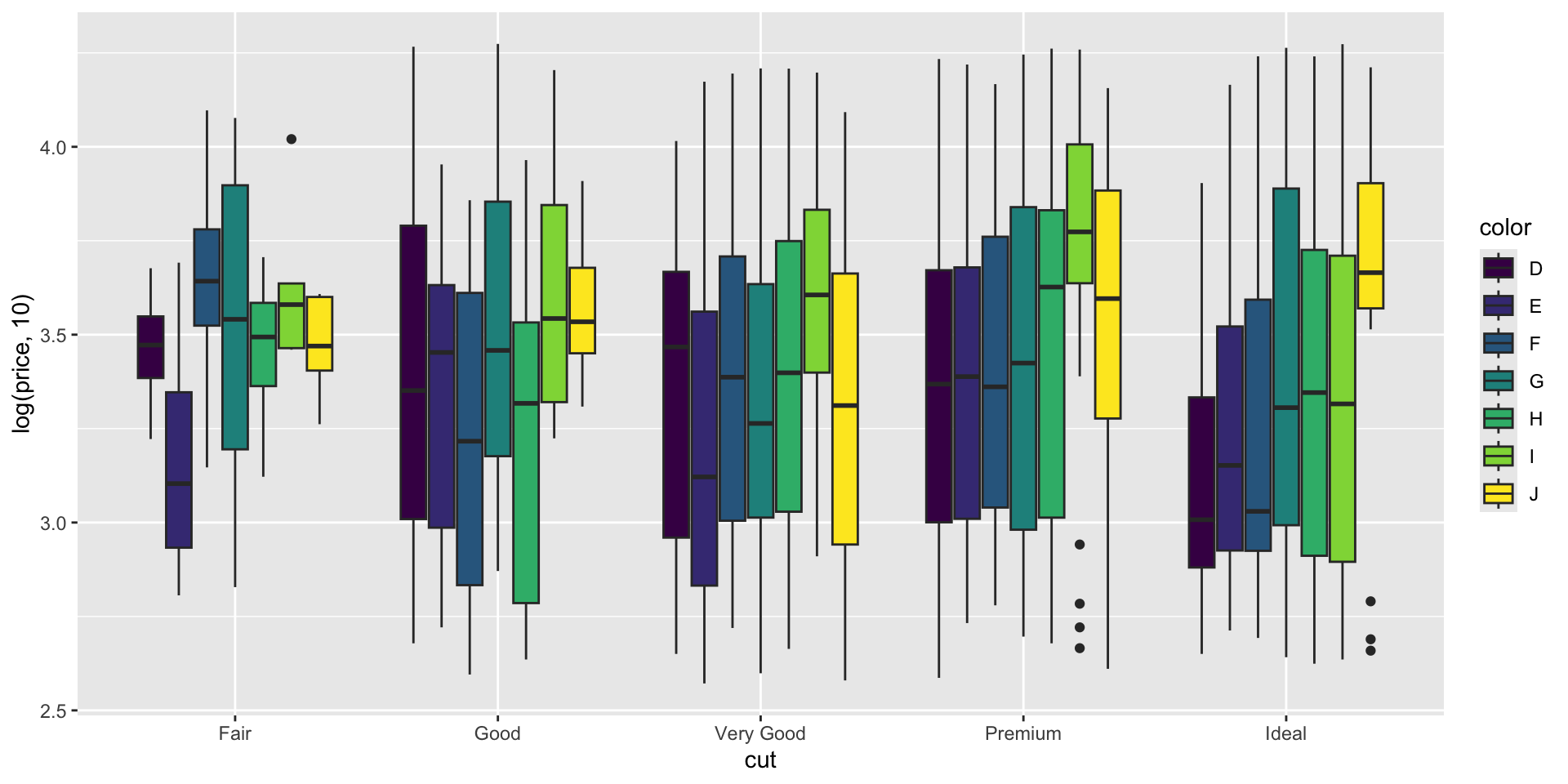
Example 5
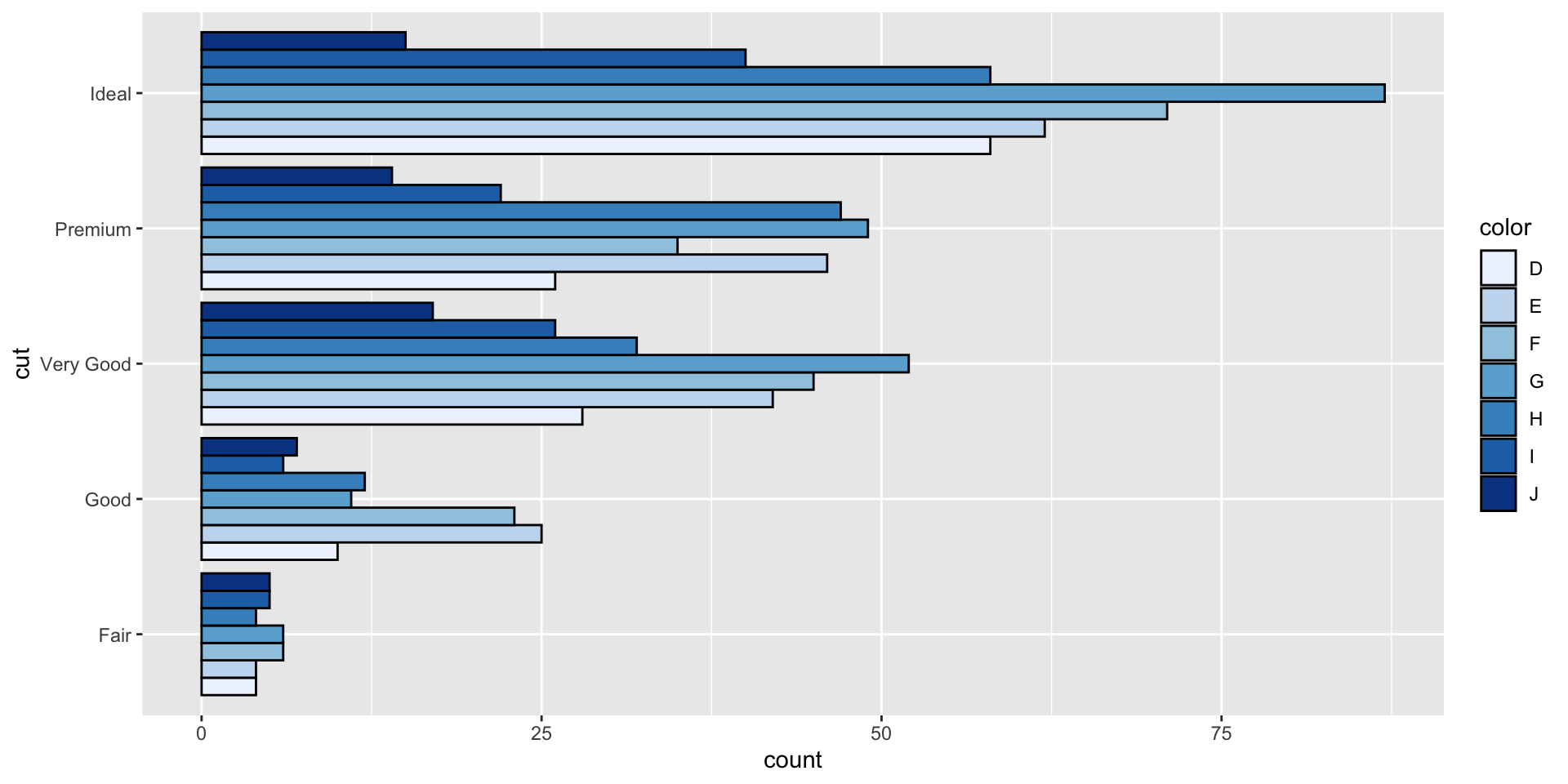
- Which data are used as an input?
- Are the variables transformed before plotting?
- What geometric objects are used to represent the data?
- What variables are mapped onto which aesthetic attributes?
- What type of scales are used to map data to aesthetics?
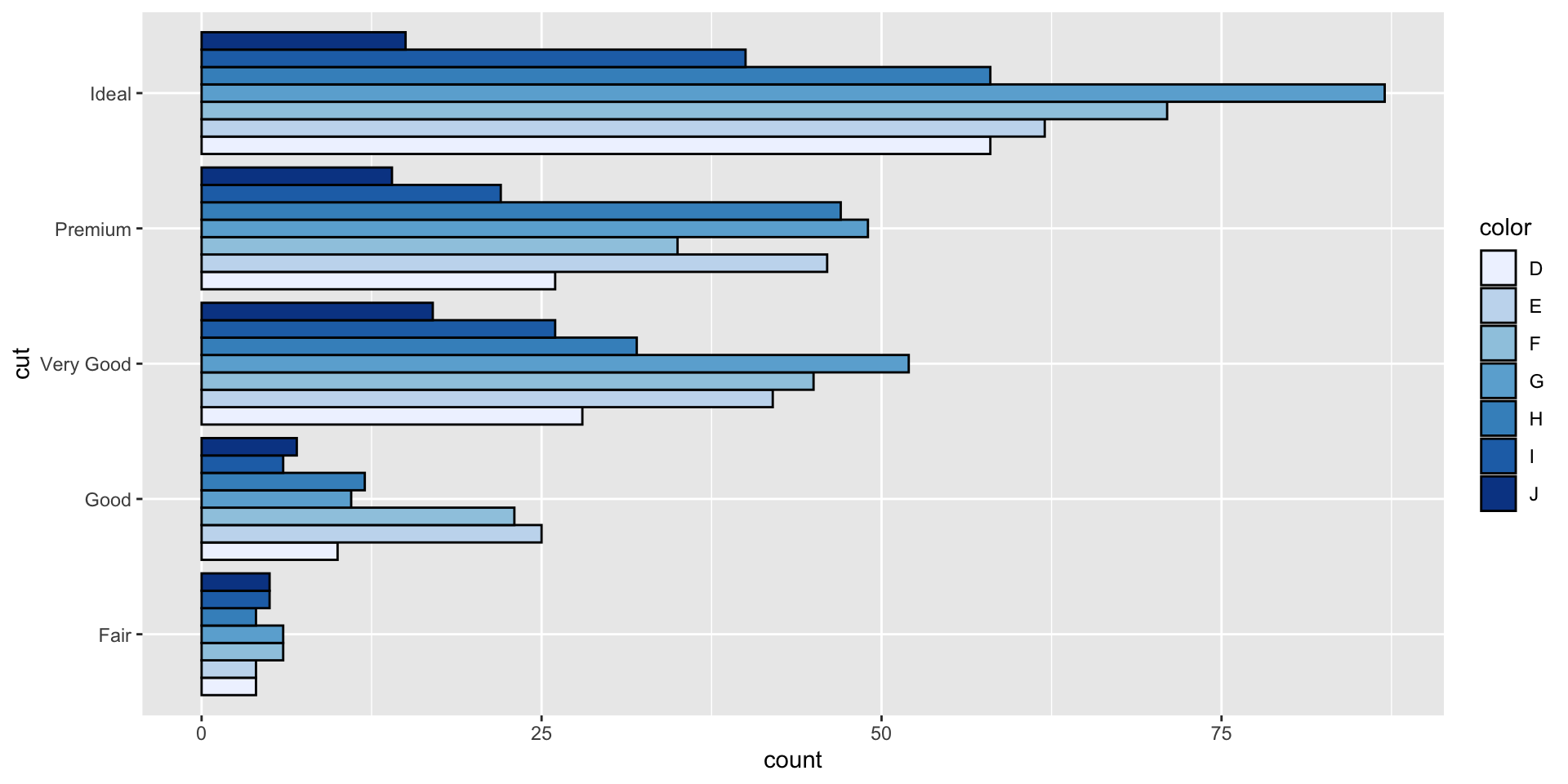
Example 6
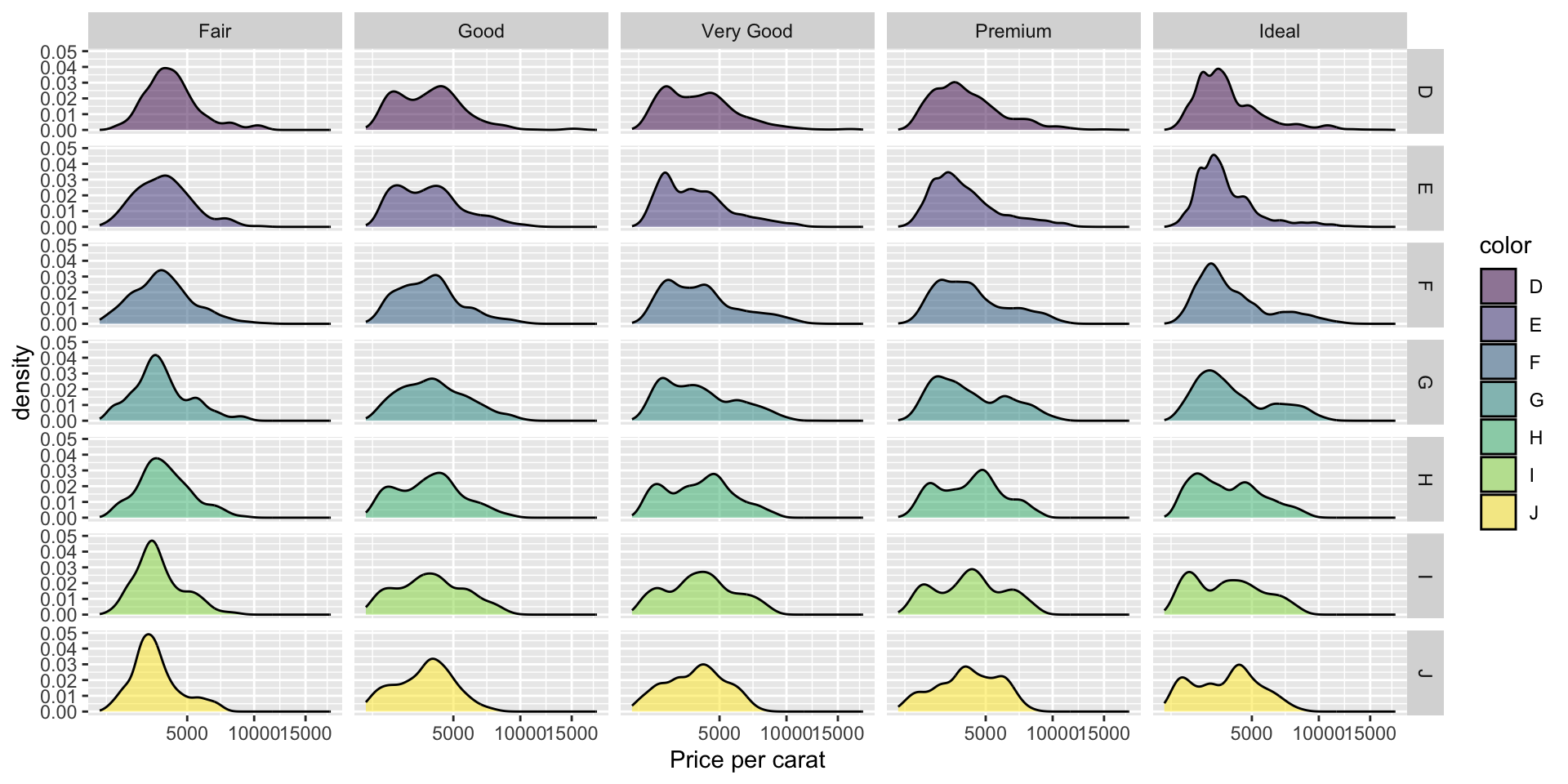
- Which data are used as an input?
- Are the variables transformed before plotting?
- What geometric objects are used to represent the data?
- What variables are mapped onto which aesthetic attributes?
- What type of scales are used to map data to aesthetics?
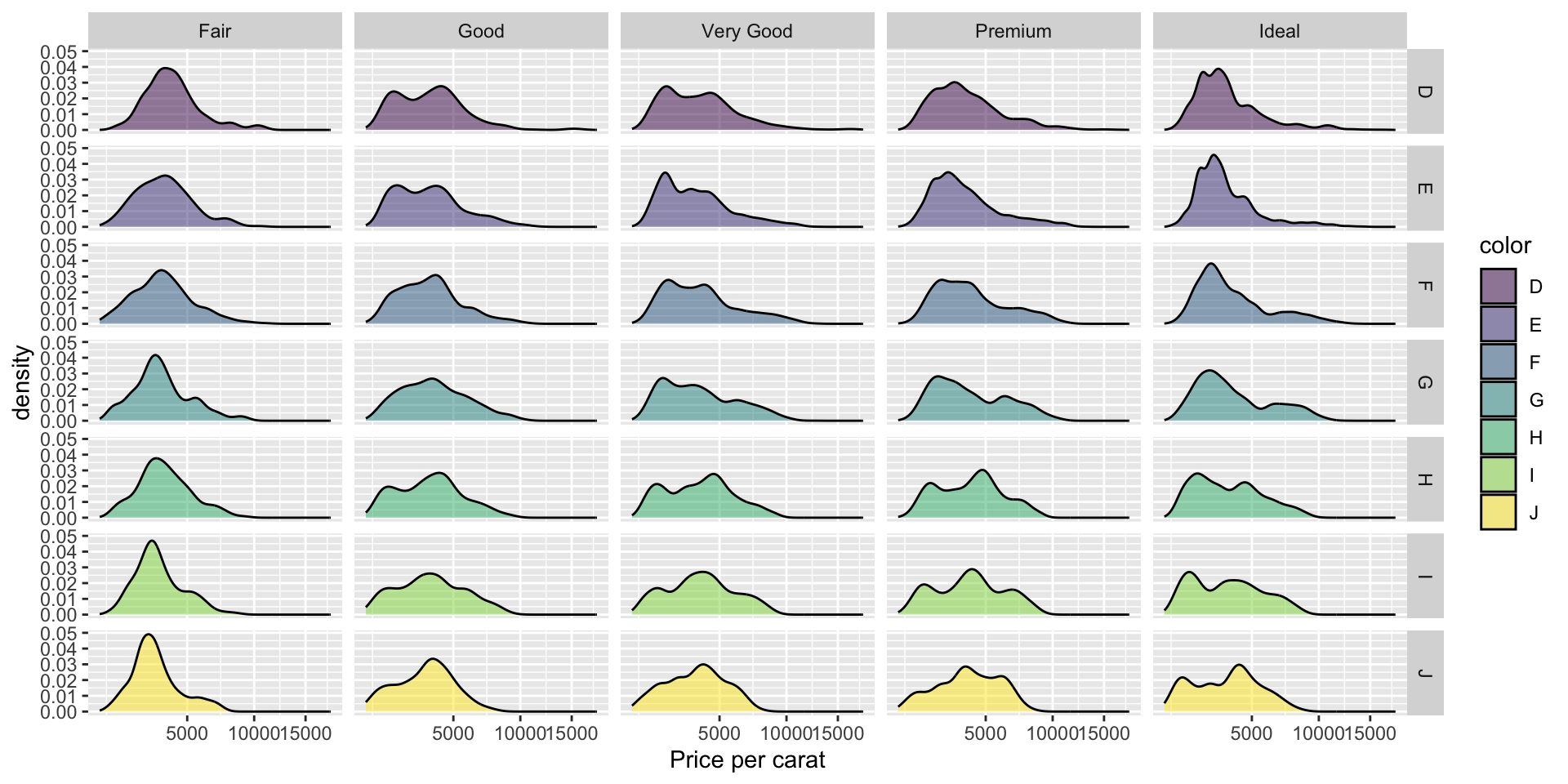
ggplot objects
Multi panel Plots
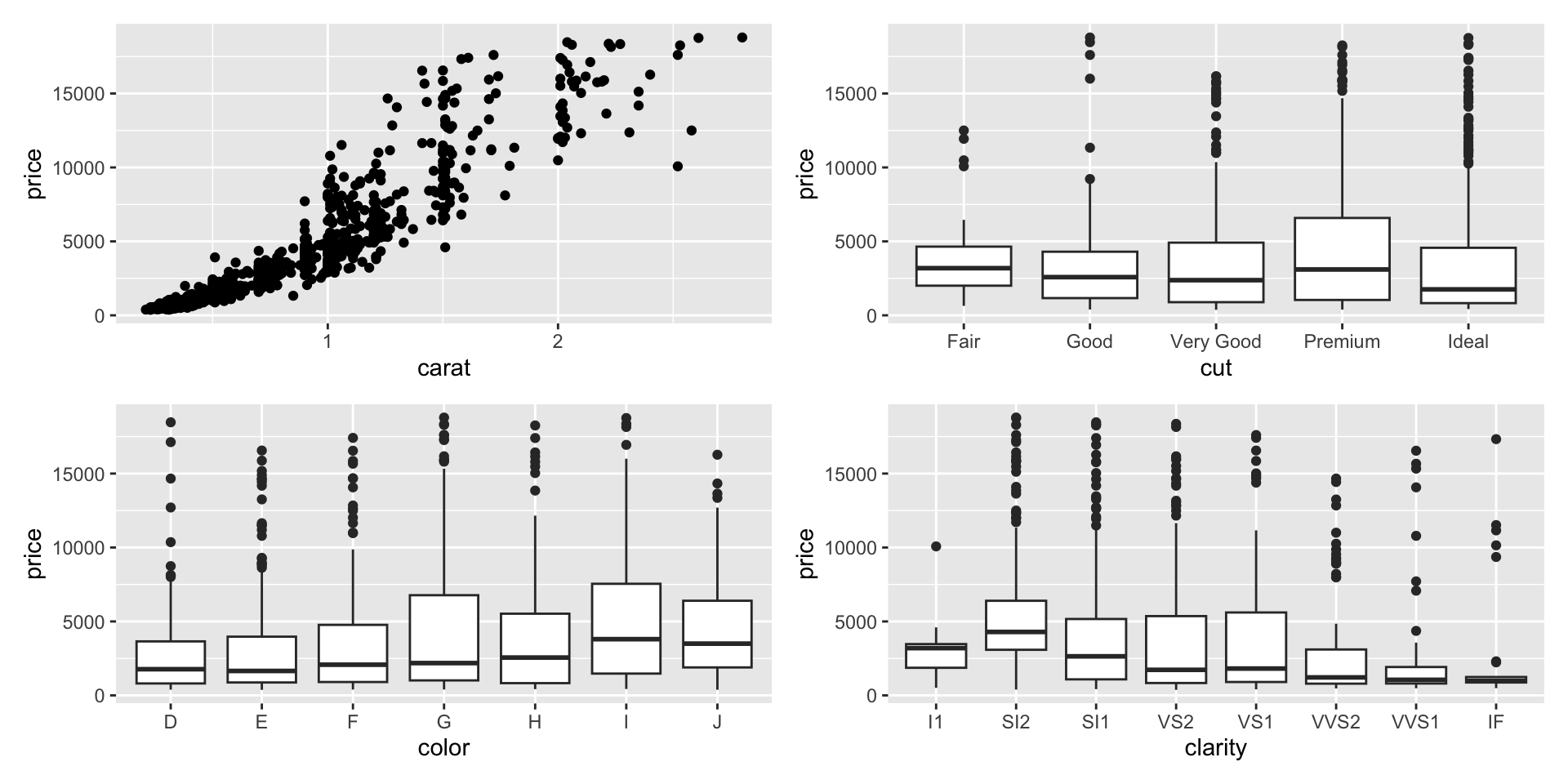
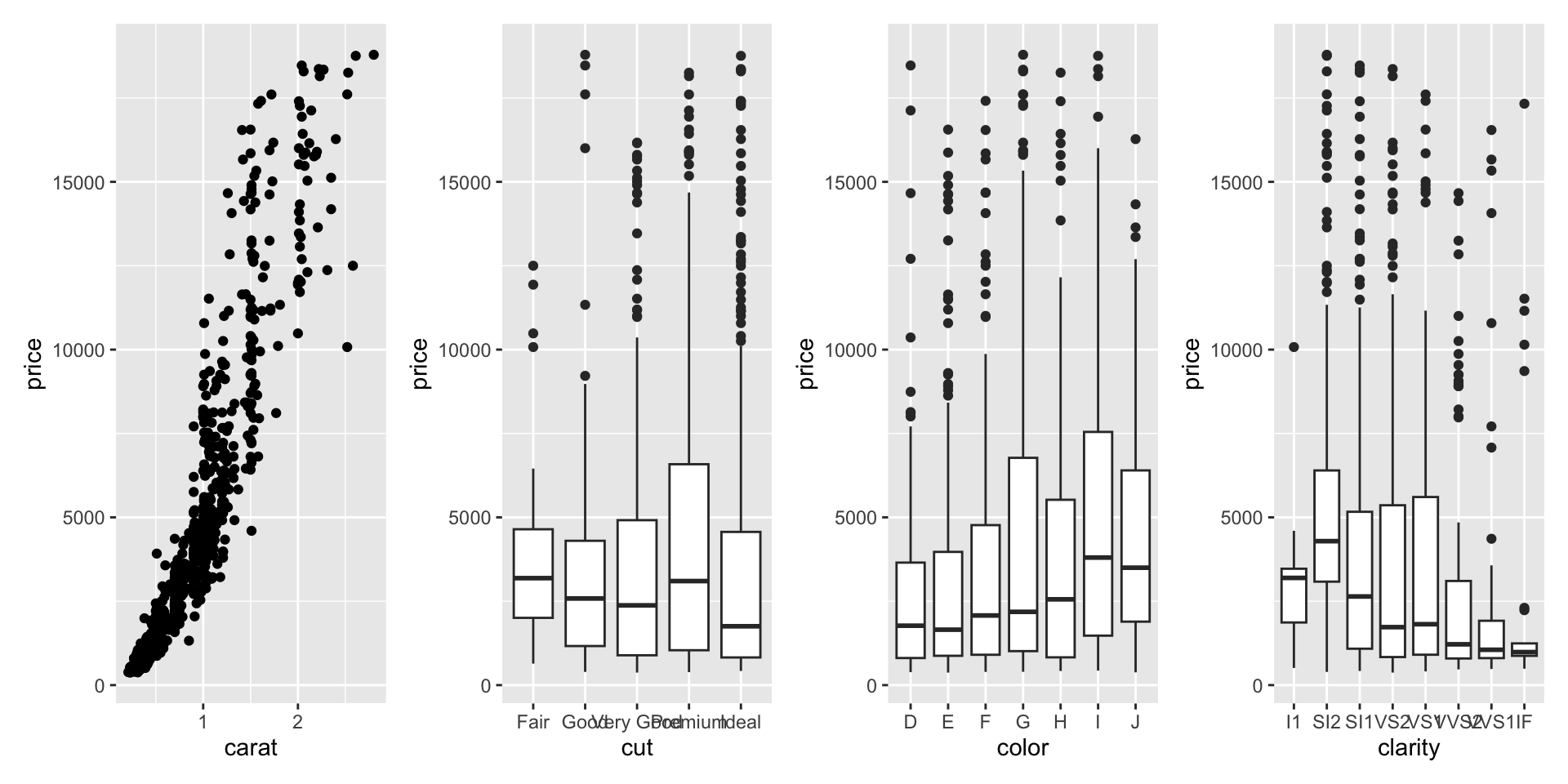
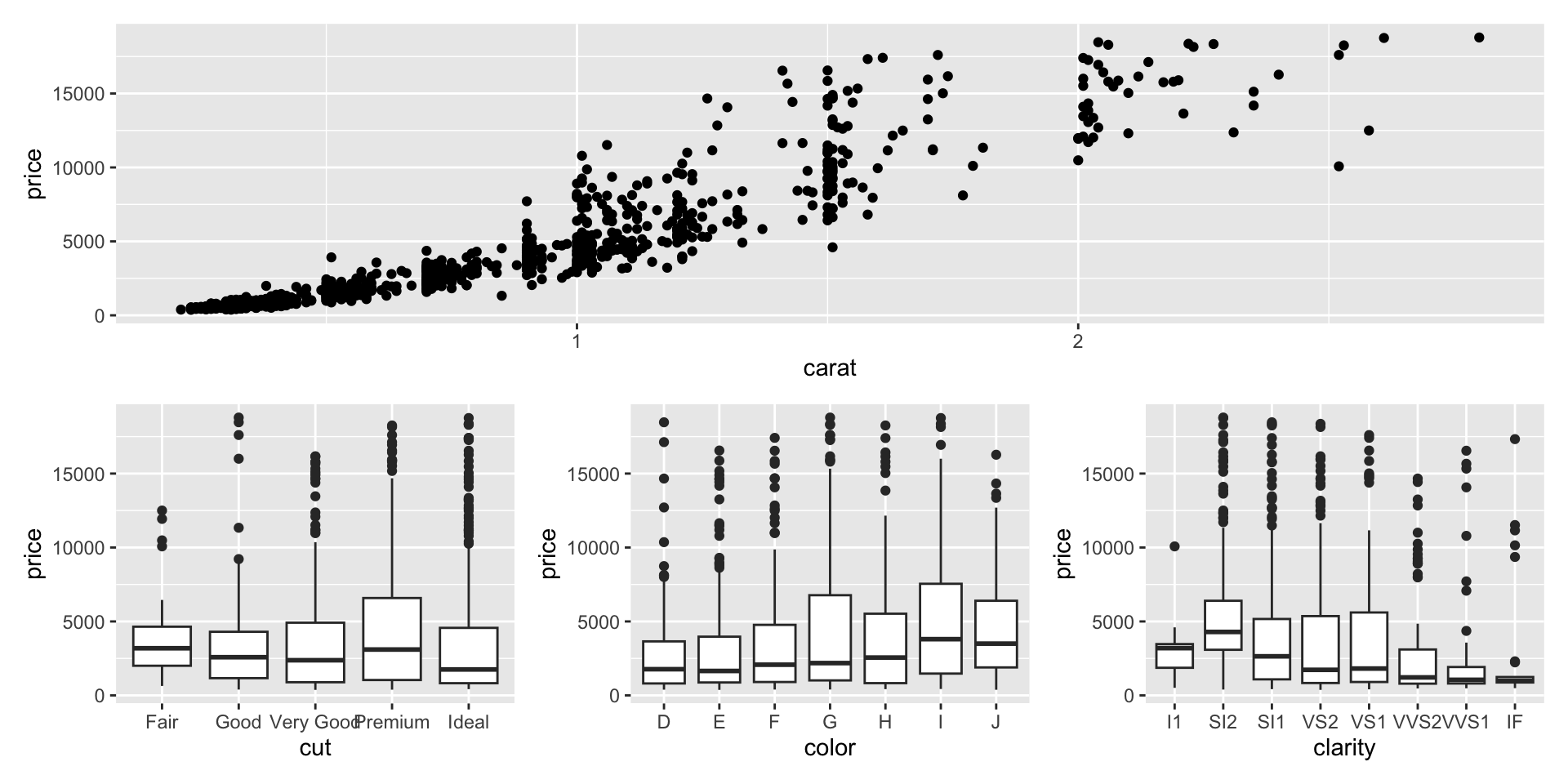
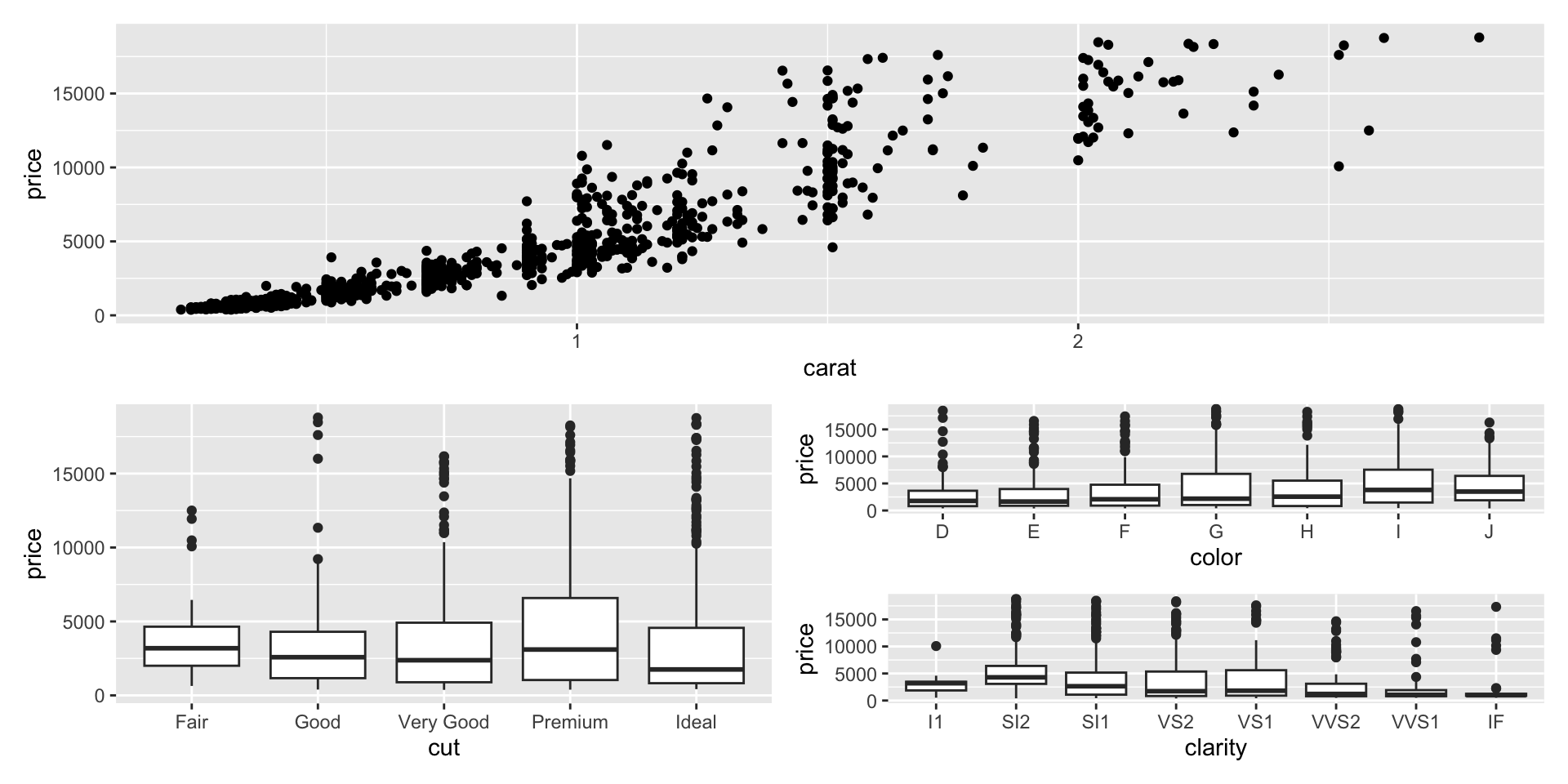
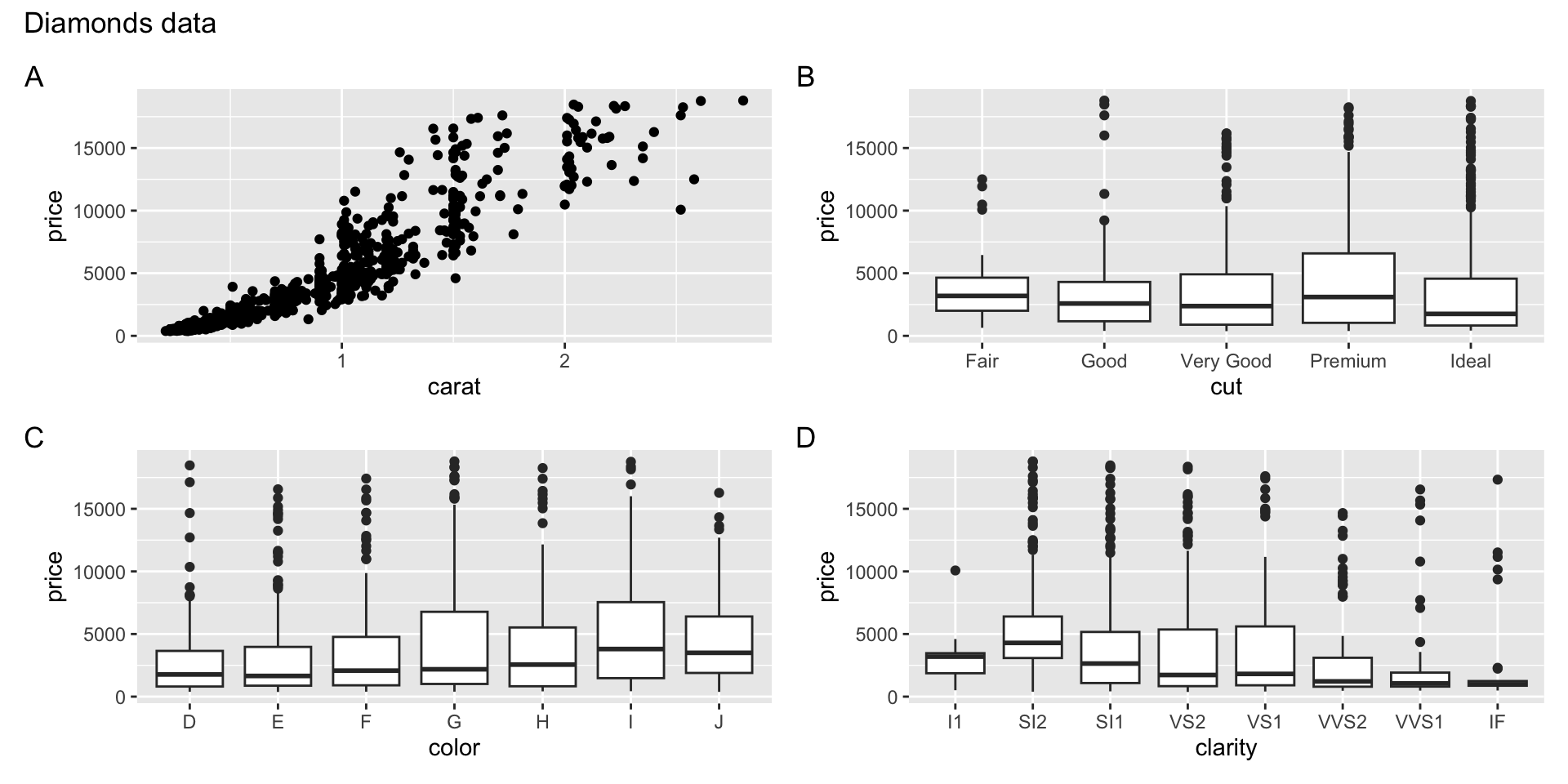
Why do we visualize?
Asncombe’s Quartet
# A tibble: 11 × 8
x1 x2 x3 x4 y1 y2 y3 y4
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 10 10 10 8 8.04 9.14 7.46 6.58
2 8 8 8 8 6.95 8.14 6.77 5.76
3 13 13 13 8 7.58 8.74 12.7 7.71
4 9 9 9 8 8.81 8.77 7.11 8.84
5 11 11 11 8 8.33 9.26 7.81 8.47
6 14 14 14 8 9.96 8.1 8.84 7.04
7 6 6 6 8 7.24 6.13 6.08 5.25
8 4 4 4 19 4.26 3.1 5.39 12.5
9 12 12 12 8 10.8 9.13 8.15 5.56
10 7 7 7 8 4.82 7.26 6.42 7.91
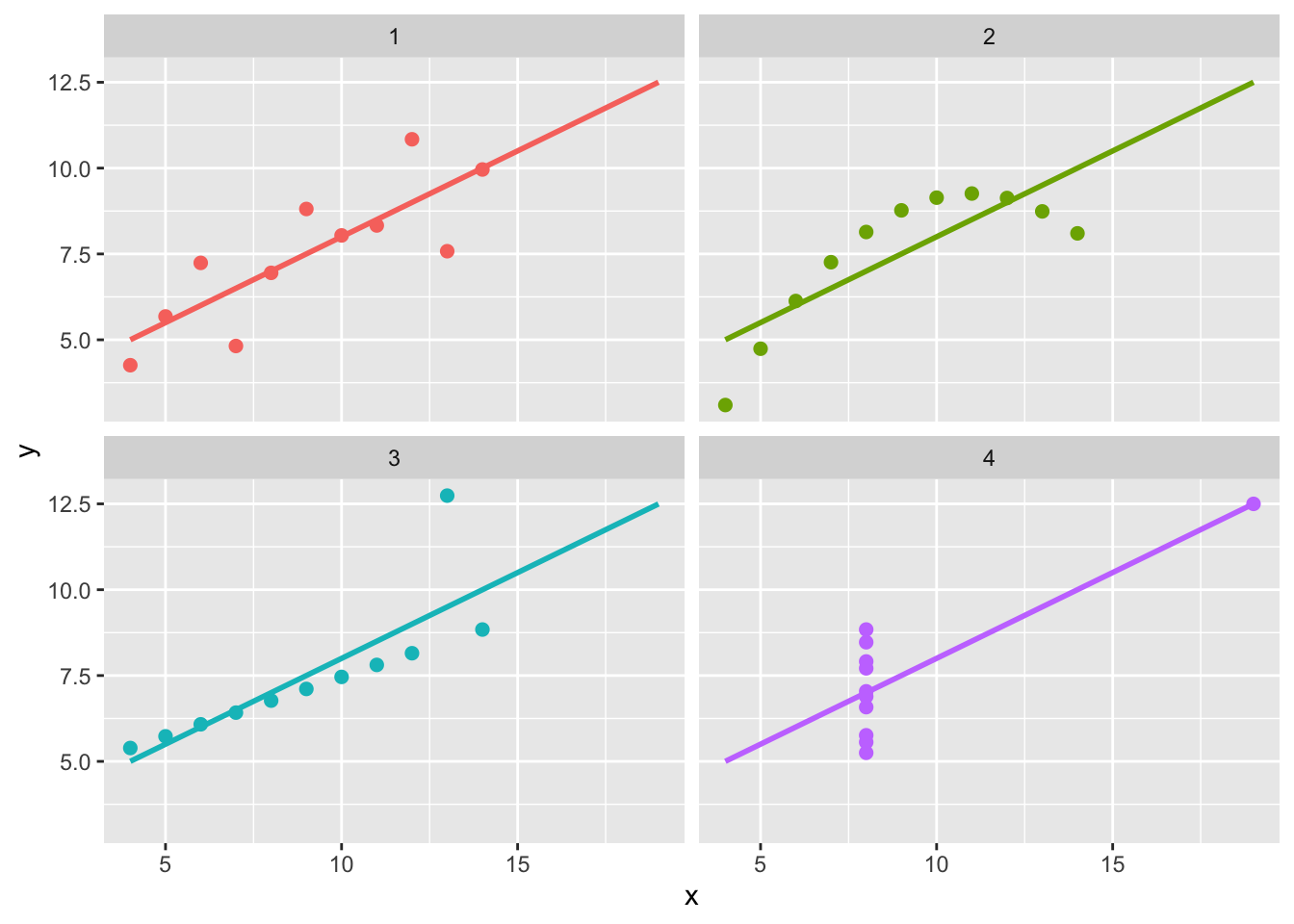
11 5 5 5 8 5.68 4.74 5.73 6.89Asncombe’s Quartet
Anscombe’s quartet comprises four datasets that have nearly identical simple descriptive statistics, yet have very different distributions and appear very different when graphed. Each dataset consists of eleven (x, y) points. They were constructed in 1973 by the statistician Francis Anscombe to demonstrate both the importance of graphing data when analyzing it, and the effect of outliers and other influential observations on statistical properties.
from: https://en.wikipedia.org/wiki/Anscombe%27s_quartet
Tidy Anscombe
Tidy Anscombe
tidy_anscombe %>%
group_by(group) %>%
summarize(mean_x = mean(x), mean_y = mean(y), sd_x = sd(x), sd_y = sd(y), cor = cor(x,y))# A tibble: 4 × 6
group mean_x mean_y sd_x sd_y cor
<chr> <dbl> <dbl> <dbl> <dbl> <dbl>
1 1 9 7.50 3.32 2.03 0.816
2 2 9 7.50 3.32 2.03 0.816
3 3 9 7.5 3.32 2.03 0.816
4 4 9 7.50 3.32 2.03 0.817Tidy Anscombe
DatasauRus
datasauRus::datasaurus_dozen %>%
group_by(dataset) %>%
summarize(mean_x = mean(x), mean_y = mean(y),
sd_x = sd(x), sd_y = sd(y),
cor = cor(x,y))# A tibble: 13 × 6
dataset mean_x mean_y sd_x sd_y cor
<chr> <dbl> <dbl> <dbl> <dbl> <dbl>
1 away 54.3 47.8 16.8 26.9 -0.0641
2 bullseye 54.3 47.8 16.8 26.9 -0.0686
3 circle 54.3 47.8 16.8 26.9 -0.0683
4 dino 54.3 47.8 16.8 26.9 -0.0645
5 dots 54.3 47.8 16.8 26.9 -0.0603
6 h_lines 54.3 47.8 16.8 26.9 -0.0617
7 high_lines 54.3 47.8 16.8 26.9 -0.0685
8 slant_down 54.3 47.8 16.8 26.9 -0.0690
9 slant_up 54.3 47.8 16.8 26.9 -0.0686
10 star 54.3 47.8 16.8 26.9 -0.0630
11 v_lines 54.3 47.8 16.8 26.9 -0.0694
12 wide_lines 54.3 47.8 16.8 26.9 -0.0666
13 x_shape 54.3 47.8 16.8 26.9 -0.0656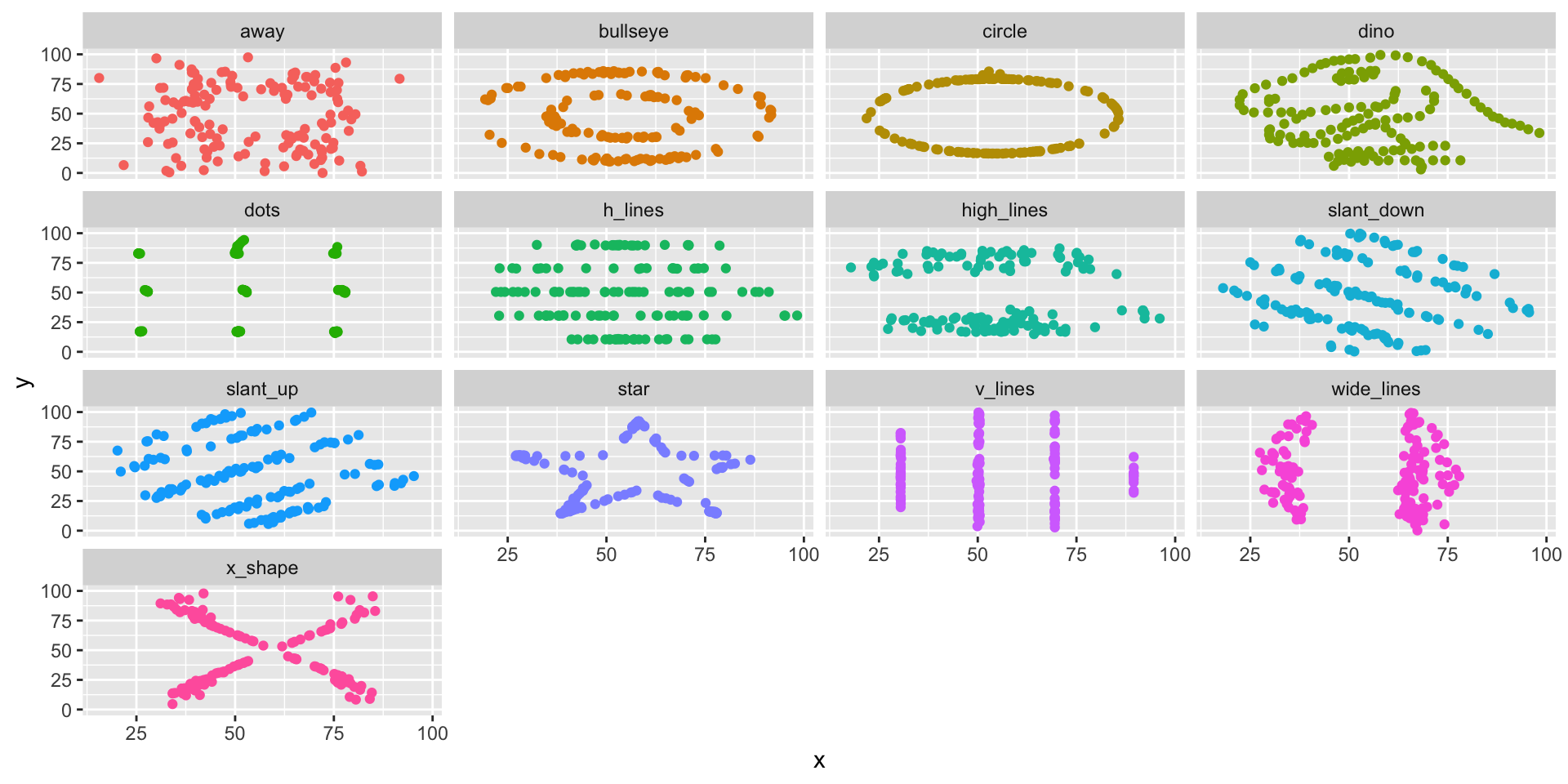
DatasauRus
The Datasaurus dozen comprises thirteen data sets that have nearly identical simple descriptive statistics to two decimal places, yet have very different distributions and appear very different when graphed. It was inspired by the smaller Anscombe’s quartet that was created in 1973.
from: https://en.wikipedia.org/wiki/Datasaurus_dozen
Resources
- ggplot2 documentation
- R Graphics Cookbook by Winston Chang
- R for Data Science by Hadley Wickham and Garrett Grolemund